
2.北京师范大学 经济与工商管理学院,北京 100875
2.Business School,Beijing Normal University,Beijing 100875,China
企业R & D投入的回报有多大?张海洋(2005)运用中国1999-2002年34个制造业行业的面板数据研究发现,R & D投入对生产率的作用不显著,甚至为负,进而认为R & D投入对企业生产率的提高并没有明显作用。Hu等(2005)运用中国1995-1999年每年约10 000个大中型制造企业数据研究发现,R & D投入产出弹性为0.027-0.029,进一步分解为高科技企业和非高科技企业,发现后者的R & D投入对生产率并没有显著影响。Jefferson等(2006)利用中国1997-1999年5 451个大中型制造企业面板数据研究发现,R & D投入产出弹性约为0.24;然而使用工具变量法时R & D投入的产出弹性却变为-0.045。李小平和朱钟棣(2006)运用1998-2003年32个制造业行业的面板数据研究发现,R & D投入对行业技术进步、技术效率和全要素生产率的增长起阻碍作用。吴延兵(2006)运用中国2002年537个四位数制造业行业数据进行研究,得到了R & D投入对生产率有显著的促进作用的结论。不过在含有中间投入的生产函数中,R & D投入的产出弹性只有0.01-0.02。周亚虹等(2012)根据全部国有和规模以上非国有工业企业数据库中2005-2007年的企业累积R & D投入量构建了知识资本存量,对2007年的生产函数进行简单OLS回归,所得到的R & D投入的产出弹性为0.02,使用工具变量的回归结果为0.04-0.06。对其他国家R & D投入回报的估计也得到类似的结论。例如,Griliches (1979)最早估计了美国制造业的R & D投入产出弹性在0.07左右; Griffith和Reenen (2006)对英国的估计结果在0.03左右。偏低甚至为负的R & D投入回报,似乎指向一个结论:R & D投入对企业发展来说无关紧要。然而,经济增长理论却赋予企业R & D投入十分重要的意义,甚至认为它是增长的发动机(Romer,1990)。本文称这个理论与经验证据间的鲜明对照为“R & D投入回报之谜”。
R & D投入回报的不确定性、非线性和企业异质性是理解“R & D投入回报之谜”的关键环节。一方面,即使平均而言R & D投入的回报并不高,但由于存在企业异质性,不排除某些企业在特定情况下R & D投入存在高额的回报,这能够为这些企业进行R & D投入提供充分的激励。另一方面,R & D投入的直接成果,即新工艺和新产品具有很强的非竞争性,对于整个行业甚至经济具有很强的外溢作用。个别企业由高额预期回报驱动的R & D活动,可能获得行业生产技术和产品方面的重大突破,甚至可以成为推动整个经济增长的重要动力(Aghion和Howitt,1992)。因此,只要R & D投入回报具有较强的企业异质性,即使平均而言R & D投入的回报并没有很高的吸引力,但也不妨碍R & D投入在宏观上对于整个经济增长具有重要意义。
然而,评估R & D投入回报的标准模型——Griliches(1979)的知识资本模型,没有考虑不确定性、非线性和企业异质性。Griliches(1979)提出在生产函数中引入技术知识当前状态的测度,它取决于企业当前和过去的R & D投入即知识资本。知识资本作为与资本和劳动对应的另一生产要素,其产出弹性可以度量R & D投入的产出回报。经验研究中一般运用永续盘存法,根据企业各年R & D支出流量序列构建出知识资本存量的代理变量,然后运用双对数模型回归出生产函数中各要素的产出弹性系数。Griliches提供了可操作的工具,随后沿着这一思路考察R & D投入回报的文献大量涌现,并且Mairesse和Sassenou(1991)、Griliches(1995、1998)、Hall等(2010)对此作了比较全面的综述。知识资本模型目前仍然是评估R & D投入产出绩效的主要工具,国内也有一些研究运用这一方法(吴延兵,2006;陆国庆,2011;周亚虹等,2012)。很明显,在知识资本模型中,R & D投入的产出弹性如同生产函数的其他参数,在构建上,行业内所有企业都是相同的。因此,如果两个企业的R & D投入序列相同,其对产出绩效的效应必然完全一样。可见知识资本框架很难令人满意地处理R & D投入回报的不确定性、非线性和企业异质性问题。
评估R & D投入产出绩效的另一常见做法是先估计企业生产率,然后用R & D投入(加上其他控制变量)对其进行回归。 容易证明,生产率的R & D投入弹性就是产出的R & D投入弹性,也即本文分析的R & D投入回报。 其中估计生产率的方法除了生产函数回归(Solow剩余)外,还包括数据包络方法(DEA)、随机前沿方法(SFA)和指数方法。如张海洋(2005)、李小平和朱钟棣(2006)均使用基于DEA的Malmquist生产率测度。这种方法在第一步估计生产率时没有充分考虑随机因素和不确定性,第二步回归在设定上假定R & D投入的产出(生产率)弹性对于所有企业都是同质的,从而仍然没有充分处理R & D投入回报的不确定性、非线性和企业异质性问题。而且,这种两步法需要应对明显的内生性挑战:R & D投入与生产率可能互为因果、可能存在同时影响两者的不可观测因素。宗庆庆等人(2013)、毛德凤等人(2013)尝试运用政策评估中的广义倾向得分匹配方法(PSM)估计R & D投入对生产率的处理效应。这仍然需要假定R & D投入和生产率间的确定性关系。
本文借鉴 Aw等(2011)以及Doraszelski和Jaumandreu (2013)的思路,将R & D投入引入企业生产率演化的马尔科夫过程,从而使其对生产率的分布产生影响,进而建立结构模型正式考虑R & D投入回报的不确定性、非线性和企业异质性问题。在他们模型的基础上,我们进行了改进,明确考虑了溢价的企业异质性,并明确处理了影响企业需求的因素。正如Klette和Griliches(1996)所指出的,不完全竞争环境下企业层面的价格还受到需求方面因素的影响,用行业水平的价格指数平减企业销售收入作为产出的代理指标,会将企业的需求异质性引入生产率估计方程,从而造成生产函数参数与生产率估计的严重偏误。 Foster等(2008)也指出,不完全竞争市场上企业异质的需求因素会造成Olley和Pakes(1996)型代理变量方法的遗漏变量偏差。也就是说,代理变量方法要求分析者所使用的不可观测到的企业生产率与其可观测到的作为生产率代理的变量必须一一对应。如果还存在其他企业层面的不可观测因素影响代理变量,Olley和Pakes(1996)型代理变量方法就会失效。如果忽视了在不完全竞争市场上的需求因素,显然会造成代理变量方法面临严重的问题。 考虑到不完全竞争环境是最近生产率文献的一个热点。例如,De Loecker(2011)在分析比利时纺织品市场贸易保护的下降对企业生产率的影响时,同时考虑了生产率异质性和需求异质性。De Loecker和 Warzynski(2012)在分析溢价与企业出口行为间的关系时,其使用企业层面数据估计溢价的方法就是建立在不完全竞争企业短期成本最小化的基础之上。我们也将Olley和Pakes(1996)、Levinsohn和Petrin(2003)以及Ackerberg 等(2006)的企业生产率结构估计思路扩展到不完全竞争环境下,同时考虑企业需求的异质性。
基于GMM的检验表明,在企业生产率演化的马尔科夫过程中引入R & D投入是很有必要的,企业本期R & D投入确实会对其下期生产率产生显著影响。进一步的检验也显示,R & D投入对企业生产率的这种影响具有不可忽视的不确定性、非线性和企业异质性。虽然平均意义上R & D投入的回报与现有文献的估计并没有明显差别,然而其确实显示出高度的不确定性和企业异质性。对所估计的生产率进行进一步分析可以得到十分明确的结果:平均而言,所有行业本期进行研发投入的企业,其下期生产率显著高于其他企业,其生产率的不确定性(方差)也更高;Kolmogorov-Smirnov检验显示,R & D投入会显著改变行业内企业的生产率分布,而且对于所有行业,进行R & D投入的企业的下期生产率分布(随机占优意义上)显著优于没有进行R & D投入的企业。这些结果表明,在考虑了影响的不确定性、非线性和企业异质性之后,中国制造业所有行业的R & D投入都显著地促进了企业生产率发展。R & D投入回报的企业异质性可以解释为什么平均意义上R & D投入的较低回报与宏观上R & D投入具有重要意义能够共存。
文章余下的结构安排是:第二部分提出结构模型和估计思路;第三部分是估计结果;第四部分对全文进行总结。
二、 R & D投入回报的结构估计企业i在t期资本存量为Kit,企业当期投入劳动Lit和中间材料Mit,其产出Yit为:
| ${Y_{it}} = {K^{{\beta _k}}}_{it}{L^{{\beta _l}}}_{it}{M^{{\beta _m}}}_{it}{e^{{\omega _{it}}}}{e^{{\mu _{it}}}}$ | (1) |
ωit为企业异质的生产率。同样的资本、劳动和中间材料投入,其产出因ωit的差异而不同。t期初企业能够观测到自己的生产率水平,但ωit对于外部分析人员而言是不可观测的。 由于缺乏企业层面的价格信息,实际产出也是外部分析人员不可观测的。 μit为企业自己也不可观测的纯粹的产出扰动。
自Olley和Pakes(1996)发表了开创性的论文以来,将企业生产率演化设定为一阶马尔科夫过程成为文献中的标准做法(例如Levinsohn和Petrin,2003;Ackerberg 等 2006;Wooldridge,2009;De Loecker,2011;De Loecker和 Warzynski,2012)。借鉴Aw 等(2011)和Doraszelski 和Jaumandreu(2013),进一步设企业R & D投入会影响其生产率演化的马尔科夫过程。具体地:
| ${\omega _{it}} = E({\omega _{it}}{\omega _{it - 1}},{\rm{ }}{r_{it - 1}}) = {\gamma _t} + g\left( {{\omega _{it - 1}},{r_{it - 1}}} \right) + {\xi _{it}}$ | (2) |
rit-1为企业上一期的R & D投入(对数)。小写字母为大写字母的对数(下同)。除共同的时间趋势γt外,企业t期的实际生产率ωit包括两个部分:企业在t-1期进行R & D投入时的期望生产率g(ωit-1,rit-1)和R & D投入后生产率的随机扰动ξit。企业t期的预期生产率取决于已经取得的生产率水平(ωit-1),也取决于上期R & D投入rit-1。这里,我们使用研发投入的流量作为研发行为的测度,主要是考虑到在模型的假设中,企业当期的生产率除了在很大程度上延续前一期生产率的惯性外,同时也与前一期的研发行为密切相关。研发投入的存量可能在长期决定企业的平均效率水平,而研发投入的流量则会更加直接地影响到企业效率演化的动态路径。另外,受到我国工业企业数据库的限制,仅凭2001年和2005-2007年这四年的研发投入流量数据也很难准确估测一个企业的研发投入存量。随机扰动ξit代表企业从R & D投入形成实际产出绩效过程中所面临的技术和市场等不确定性。企业R & D投入对生产率的影响及其不确定性、非线性和企业异质性正是通过这种方式得以模型化。企业是了解其g(ωit-1,rit-1)的,但它对于外部分析人员而言却是不可观测的。
根据式(1)和式(2),可以看到$\frac{{\partial g\left( {{\omega _{it}},{r_{it - 1}}} \right)}}{{\partial {r_{it - 1}}}}$即为R & D投入的期望产出弹性(边际),本文称为R & D投入的边际弹性。另外,如果我们沿用先估计出生产率ωit,然后用rit-1对其进行回归的传统思路,rit-1的系数即为R & D投入的实际产出弹性(平均),本文称为R & D投入的平均弹性。从而在这个意义上,R & D投入对企业生产率的影响和R & D投入的产出绩效是一回事。估计出了ωit和条件期望函数g(ωit-1,rit-1),R & D投入的产出绩效评估问题就迎刃而解了。
很多企业(至少在部分年度)不进行R & D投入。例如在我们分析的样本中,R & D投入为正的企业所占比重一般只有4.85%-22.11%。基于这样的事实,我们借鉴Doraszelski和Jaumandreu(2013)的研究,允许有R & D投入和没有R & D投入企业的生产率的演化规律存在差异,即有不同的条件期望函数g(ωit-1,rit-1)。具体地:
| $\begin{array}{l} g\left( {{\omega _{it - 1}},{r_{it - 1}}} \right) = 1\left( {{R_{it - 1}} = 0} \right)\left( {{g_{00}} + {g_{01}}\left( {{\omega _{it - 1}}} \right)} \right)\\ + 1\left( {{R_{it - 1}} > 0} \right){\rm{ }}{g_{10}} + {g_{11}}\left( {{\omega _{it - 1}},{r_{it - 1}}} \right)] \end{array}$ | (3) |
1(Rit-1=0)和1(Rit-1>0)分别为不进行R & D投入和进行R & D投入的示性函数。
与Doraszelski和Jaumandreu(2013)的研究不同,我们明确处理企业需求价格弹性的异质性,并控制引起需求曲线移动的因素。具体地,设市场是垄断竞争的,企业i面临如下Dixitt-Stiglitz型需求函数:①
| ${P_{it}} = {\Phi _t}\left( {{Y_{it}}} \right){^{\frac{1}{{{\eta _i}}}}}{e^{h{\rm{ }}\left( {{A_{it}}} \right)}}{e^{{\zeta _{it}}}}$ | (4) |
Pit为企业产出价格,Φt反映t期总的市场特征,ηi>0为企业异质的需求弹性(绝对值)。企业可以通过加强广告营销、改善售后服务等销售努力(Ait),提高消费者对其产品的评价,从而移动其需求曲线。h(·)为未知函数。ζit为需求扰动。
这样,观察到的企业实际销售收入(取对数)为:
| $re{{v}_{it}}={{\varphi }_{t}}+\left( 1-\frac{1}{{{\eta }_{i}}} \right)\left( {{\beta }_{k}}{{k}_{it}}+{{\beta }_{l}}{{l}_{it}}+{{\beta }_{m}}{{m}_{it}}~ \right)~+h\text{ }\left( {{A}_{it}}~ \right)+\text{ }\left( 1-\frac{1}{{{\eta }_{i}}} \right){{\omega }_{it}}+{{\upsilon }_{it}}$ | (5) |
${\upsilon _{it}} = \left( {1 - \frac{1}{{{\eta _i}}}} \right){\mu _{it}} + {\xi _{it}}$。企业每期劳动和中间材料可以充分(无成本)调整,从而当期劳动和中间材料选择只影响当期利润。企业t期选择Lit和Mit最大化当期税后利润,根据中间材料的一阶条件:
| ${{\omega }_{it}}=\text{ }\frac{{{\eta }_{i}}~}{{{\eta }_{i}}-1}\left[ \begin{array}{*{35}{l}} {{p}_{Mt}}-{{\varphi }_{t}}-\ln {{\beta }_{m}}-\left( 1-\frac{1}{{{\eta }_{i}}} \right)+\left( \frac{1}{{{\eta }_{i}}}-1 \right){{\beta }_{k}}{{k}_{it}}+\left( \frac{1}{{{\eta }_{i}}}-1 \right){{\beta }_{l}}{{l}_{it}} \\ +\left( \frac{1}{{{\eta }_{i}}}{{\beta }_{m}}-{{\beta }_{m}}+1 \right){{m}_{it}}-h\left( {{A}_{it}}~ \right)-\ln \left( 1-{{\tau }_{it}} \right) \\ \end{array} \right]$ | (6) |
τit为销售税率。由于地区间税收优惠政策和税收努力程度的差别,这里设定税率是企业异质的。本文的任务是根据式(2)、式(3)、式(5)和式(6),估计生产函数式(1)和需求函数式(4)的参数,进而识别出企业实际生产率ωit和期望生产率(条件期望函数)g(ωit-1,rit-1)。
将式(2)和式(3)代入式(5),用Ait的三阶多项式逼近未知函数h (Ait) ;用ωit-1的三阶多项式逼近未知函数g01(ωit-1);用ωit-1和rit-1的三阶多项式逼近未知函数g11(ωit-1,rit-1),复合误差项可以表示成:
| $\begin{align} & {{{\hat{\varphi }}}_{it}}=re{{\upsilon }_{it}}-\left( 1-\frac{1}{{{\eta }_{i}}} \right)\left( {{\beta }_{k}}{{k}_{it}}+{{\beta }_{l}}{{l}_{it}}+{{\beta }_{m}}{{m}_{it}} \right)-{{a}_{1}}{{A}_{it}}-{{a}_{2}}A_{it}^{2}-{{a}_{3}}A_{it}^{3}-{{p}_{t}} \\ & -{{c}_{0}}-\left( c+{{\gamma }_{1}}\cdot {{d}_{07}}+{{\gamma }_{2}}\cdot {{d}_{08}} \right)\left( 1-\frac{1}{{{\eta }_{i}}} \right)-1\left( {{R}_{it-1}}=0 \right) \\ & \left( 1-\frac{1}{{{\eta }_{i}}} \right)\left[ {{g}_{01}}\left( {{\omega }_{it-1}} \right) \right]-1\left( {{R}_{it-1}}>0 \right)\left( 1-\frac{1}{{{\eta }_{i}}} \right)\left[ {{g}_{1}}+{{g}_{11}}\left( {{\omega }_{it-1}},{{r}_{it-1}} \right) \right] \\ \end{align}$ | (7) |
我们用行业一般价格水平pt代理总市场特征φt。d07和d
| ${{{\hat{\omega }}}_{it-1}}=\frac{{{\eta }_{i}}~}{{{\eta }_{i}}-1}\left[ \begin{array}{*{35}{l}} {{p}_{Mt-1}}-{{p}_{t-1}}-\ln \left( 1-\frac{1}{{{\eta }_{i}}} \right)+\left( \frac{1}{{{\eta }_{i}}}-1 \right){{\beta }_{k}}{{k}_{it-1}}+\left( \frac{1}{{{\eta }_{i}}}-1 \right){{\beta }_{l}}{{l}_{it-1}} \\ +\left( \frac{1}{{{\eta }_{i}}}{{\beta }_{m}}-{{\beta }_{m}}+1 \right){{m}_{it-1}}-{{a}_{1}}{{A}_{it-1}}-{{a}_{2}}A_{it-1}^{2}-{{a}_{3}}A_{it-1}^{3}-\ln \left( 1-{{\tau }_{it}} \right) \\ \end{array} \right]$ | (8) |
lnβm和h(·)中的常数项被吸收到式(7)中的对应部分。式(7)和式(8)构成本文的基本估计方程。给定待估参数向量θ,可以得到式(7)的残差为${{\hat \varphi }_{it}}\left( \theta \right)$。这样参数估计的GMM问题为:
| $\underset{\theta }{\mathop{\min }}\,\left[ \frac{1}{N}\sum\limits_{i,t}{{{Z}_{it}}{{{\hat{\varphi }}}_{it}}\left( \theta \right)} \right]\prime {{W}_{N}}\left[ \frac{1}{N}\sum\limits_{i,t}{{{Z}_{it}}{{{\hat{\varphi }}}_{it}}\left( \theta \right)} \right]$ | (9) |
WN为权重矩阵,N为总观测数。我们运用Hansen(1982)的二阶段GMM估计。第一阶段使用权重矩阵${W_N} = {\left[ {\frac{1}{N}\sum\limits_{i,t} {{Z_{it}}Z_{it}^\prime } } \right]^{ - 1}}$,得到θ的一致估计θ,以及ψit(θ)。第二阶段使用权重矩阵${W_N} = {\left[ {\frac{1}{N}\sum\limits_{i,t} {{Z_{it}}{\varphi _{it}}\left( \theta \right){\varphi _{it}}{{\left( \theta \right)}^\prime }} Z_{it}^\prime } \right]^{ - 1}}$,得到最优估计${\hat \theta }$。
式(7)和式(8)中需要估计的参数有23个:3个常数(c0,c和g00);2个生产率演化的时间趋势(γ1和γ2);3个生产函数参数(βk,βl和βm);未知函数h (·) 的3个参数(a1,a2和a3);未知函数g01(·)的3个参数;以及未知函数g11(·)的9个参数。运用GMM估计时,θ中并不需要包括所有23个参数,根据Doraszelski和Jaumandreu(2013)提出的“Concentrate out”方法,从式(7)和式(8)可见θ中只需要包括βk、βl、βm、a1,a2和a3,其他17个参数可以用这6个参数线性表示。这大大减少了GMM估计过程中非线性的程度,提高了算法的搜索效率。
根据Newey(1990,1993)的最优工具理论,我们使用的工具变量共47个,包括常数,时间虚拟变量(2个),销售努力的三阶多项式(滞后1期,3个),R & D投入量(对数)的三阶多项式(滞后1期,3个),有R & D投入(虚拟变量)与资本、劳动和中间材料完全三阶多项式的交互(滞后1期,19个),无R & D投入(虚拟变量)与资本、劳动和中间材料完全三阶多项式的交互(滞后1期,19个)。
①这是生产率估计中广泛使用的需求函数,例如Aw 等(2011)和DeLoecker(2011)。
三、 估计结果本文所用数据来自国家统计局“全部国有和规模以上非国有工业企业数据库”,时间涉及1998-2008年。参照Brandt等(2012)的研究,本文对这套数据库进行了细致的匹配,尽量构建合理的面板(整理过程参见尹恒和杨龙见(2014))。 由于篇幅限制,所用变量的定义与构建未列出,如有需要可向作者索要。 由于只有2001年、2005-2007年存在R & D投入数据,而估计过程中需要用到滞后一期的变量,所以本文最终使用的样本期为2005-2008年,包括所有在此期间至少存在连续两年完整数据的企业。本文的行业定义参考Doraszelsk和Jaumandreu(2013),将二位数行业合并为10个行业。②
②由于篇幅限制,行业对应代码、主要变量的统计描述以及相应的附录均未列出,如有需要可以向作者索要。
1.参数估计结果和模型设定检验
以上理论模型和结构设定是否符合中国制度背景?或者说这些估计设定能否较好地契合中国特定时期的数据产生过程? 这是事关R & D投入回报估计结果可靠性和可信性的关键问题。为此我们先讨论基本参数估计结果的合理性,并根据GMM估计的特性检验模型的关键设定。
表 1报告了所有10个行业的生产函数和需求函数的参数估计。可以看到,各行业资本、劳动和中间材料的弹性均处在合理的范围内,且都相当显著。长期规模收益(资本、劳动和中间材料弹性之和)在0.9-1.1之间,短期规模收益(劳动和中间材料弹性之和)在0.9左右,与文献的标准结果是一致的(Doraszelski和Jaumandreu,2013)。各行业的平均溢价在1.1左右,这是文献中溢价的标准估计结果(Aw等,2011;De Loecker和Warzynski,2012)。大部分行业销售努力的一次项显著为正,考虑到销售努力处于0-1之间,可以看到,销售努力对需求的边际效应也是正的,这表明销售努力的加大确实能够使企业的需求曲线向外移。
| 行业 | 生产函数 | 销售努力 | 溢价 | 函数值 | ||||
| 资本 | 劳动 | 材料 | 1次项 | 2次项 | 3次项 | |||
| 1 | 0.146 | 0.232 | 0.619 | 4.908 | 1.054 | 0.227 | 1.121 | 322.717 |
| (0.009) | (0.023) | (0.022) | (2.845) | (29.864) | (85.784) | |||
| 2 | 0.129 | 0.140 | 0.729 | 9.760 | -13.982 | -4.126 | 1.080 | 197.809 |
| (0.005) | (0.022) | (0.022) | (3.372) | (74.239) | (291.279) | |||
| 3 | 0.130 | 0.114 | 0.768 | 6.015 | -14.767 | -3.333 | 1.104 | 42.983 |
| (0.013) | (0.037) | (0.035) | (4.741) | (70.621) | (210.222) | |||
| 4 | 0.107 | 0.207 | 0.705 | 3.839 | 15.100 | 3.677 | 1.107 | 111.607 |
| (0.015) | (0.040) | (0.029) | (4.147) | (81.199) | (270.965) | |||
| 5 | 0.160 | 0.343 | 0.580 | -57.770 | 469.836 | -857.805 | 1.126 | 185.631 |
| (0.009) | (0.022) | (0.026) | (3.007) | (35.826) | (104.655) | |||
| 6 | 0.106 | 0.100 | 0.739 | 11.521 | -61.319 | 101.264 | 1.110 | 165.501 |
| (0.008) | (0.018) | (0.020) | (3.409) | (48.920) | (128.926) | |||
| 7 | 0.061 | 0.560 | 0.477 | -10.851 | 22.377 | 7.738 | 1.114 | 513.875 |
| (0.008) | (0.020) | (0.017) | (5.173) | (81.538) | (317.885) | |||
| 8 | 0.107 | 0.096 | 0.819 | 4.497 | -3.900 | -0.881 | 1.117 | 123.523 |
| (0.007) | (0.015) | (0.015) | (1.220) | (22.657) | (83.124) | |||
| 9 | 0.134 | 0.103 | 0.786 | 6.922 | -6.428 | -2.544 | 1.105 | 61.387 |
| (0.013) | (0.031) | (0.029) | (2.836) | (50.459) | (167.712) | |||
| 10 | 0.141 | 0.118 | 0.795 | -1.332 | 61.837 | 6.951 | 1.118 | 152.102 |
| (0.009) | (0.024) | (0.022) | (2.328) | (42.011) | (160.179) | |||
| 注:1.括号中为标准差;2.溢价为行业内企业的简单平均(未加权)。 | ||||||||
下面检验是否有必要在模型中考虑R & D投入对期望生产率演化的影响,即模型的设定式(2)和式(3)是否能得到数据的支持。这是本文R & D投入回报估计模型的关键设定。如果企业生产率演化的真实过程如下:
| ${{\omega }_{it}}=g\left( {{\omega }_{it-1}} \right)+{{\xi }_{it}}~$ | (10) |
其中,R & D投入并不影响企业生产率演化的马尔科夫过程,那么整个论文的分析思路就不成立。反之,如果真实情况是式(2)和式(3),但在模型误设为式(10)时,R & D投入对下一期生产率的影响将进入ξit项。此时在结构估计中即便使用滞后期变量为工具,残差项中包含的滞后期的R & D投入也很可能与滞后期的工具变量相关,导致矩条件E =0失效,从而导致估计偏误。为此我们对基本模型进行参数约束检验。无约束模型为考虑R & D投入的式(2),有约束模型为式(10),即R & D投入对应的参数都为0。根据GMM的基本理论,有约束模型和无约束模型采用同一个最优权重矩阵得到的最小化目标函数值之差,经过样本量的调整后服从开方分布,其自由度就是约束的个数。原假设是式(10)成立。据表 2所示,所有行业最小化的目标函数值之差是显著的,这表明原假设被拒绝,R & D投入对企业生产率的演化存在显著影响,即式(2)和式(3)设定是合理的。
| 行业 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| χ2 | 172.864 | 62.500 | 18.960 | 28.646 | 331.827 | 52.745 | 36.300 | 43.209 | 20.276 | 265.044 |
| p值 | 0.000 | 0.000 | 0.041 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.027 | 0.000 |
| 注:开方分布的自由度为10。 | ||||||||||
估计基本模型时,我们用三阶多项式来逼近期望生产率函数,以考虑R & D投入对期望生产率影响的非线性。即设定:
| $\begin{align} & {{g}_{11}}\left( {{\omega }_{it-1}},{{r}_{it-1}} \right)={{\alpha }_{1}}{{\omega }_{it-1}}+{{\alpha }_{2}}{{\omega }^{2}}_{it-1}+{{\alpha }_{3}}{{\omega }^{3}}_{it-1}+{{\alpha }_{4}}{{r}_{it-1}}+{{\alpha }_{5}}{{r}^{2}}_{it-1}+{{\alpha }_{6}}{{r}^{3}}_{it-1} \\ & +{{\alpha }_{7}}{{\omega }_{it-1}}{{r}_{it-1}}+{{\alpha }_{8}}{{\omega }^{2}}_{it-1}{{r}_{it-1}}+{{\alpha }_{9}}{{\omega }_{it-1}}{{r}^{2}}_{it-1} \\ \end{align}$ | (11) |
这种非线性的逼近是否必要?或者说R & D投入对期望生产率影响是否具有非线性?具体地,若原假设:
| ${{\alpha }_{5}}={{\alpha }_{6}}={{\alpha }_{7}}={{\alpha }_{8}}={{\alpha }_{9}}=0$ | (12) |
成立,则R & D投入对期望生产率的影响是线性的。这也是一个线性约束检验,我们用同样的方法检验,结果见表 3。可以看到,10个制造业行业中有8个十分显著,原假设被拒绝,R & D投入对期望生产率的影响是非线性的。值得注意的是行业3(木材和家具制造业)不能拒绝R & D投入对期望生产率的影响主要是线性的。 我们仍然采用设定式(11)对这个行业进行估计。即使原假设成立,用设定式(11)进行估计只是扩大了估计参数集,参数估计的一致性不受影响。
| 行业 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| χ2 | 150.598 | 36.502 | 1.536 | 13.021 | 46.037 | 27.477 | 28.507 | 18.822 | 9.368 | 224.865 |
| p值 | 0.000 | 0.000 | 0.957 | 0.043 | 0.000 | 0.000 | 0.000 | 0.005 | 0.154 | 0.000 |
| 注:开方分布的自由度为6。 | ||||||||||
在式(2)中ξit代表企业生产率演化过程中面临的随机冲击,我们可以进一步用ξit方差与实际生产率方差之比 $\frac{{{\mathop{\rm var}} \left( {{\xi _{it}}} \right)}}{{{\mathop{\rm var}} \left( {{\omega _{it}}} \right)}}$衡量R & D投入影响的不确定性。表 4的结果表明,对于所有行业,在生产率演化路径中企业不可控制的随机扰动ξit占整个生产率变动的比重不可忽视,R & D投入对企业实际生产率的影响确实存在很强的不确定性。即便对于不能拒绝线性影响的行业3(木材和家具制造业),这种不确定性也是明显的。
| 行业 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $\frac{{{\mathop{\rm var}} \left( {{\xi _{it}}} \right)}}{{{\mathop{\rm var}} \left( {{\omega _{it}}} \right)}}$ | 0.503 | 0.345 | 0.192 | 0.181 | 0.471 | 0.273 | 0.336 | 0.350 | 0.216 | 0.865 |
总之,参数估计结果都在合理的范围内,检验结果支持我们关于R & D投入影响生产率演化机制的设定,也支持这种影响的不确定性和非线性的设定。这为我们以下的分析提供了可靠的基础。
2.R & D投入对企业生产率分布的影响
下面讨论总体R & D投入对企业生产率的影响。表 5列示了研发企业和无研发企业生产率的均值和方差差异。表 5左半部分显示,平均而言,所有行业上期进行R & D的企业都具有更高的生产率。t检验表明两组企业的差距十分显著。表 5右半部分表明,所有行业进行R & D的企业下期生产率的标准差更大,F检验显示差距十分显著。这进一步说明了R & D投入回报的不确定性。
| 行业 | 生产率均值差异检验 | 生产率标准差差异检验 | ||||||
| 无研发 均值 | 有研发 均值 | 有研发企业 TFP均值更高 | 无研发 标准差 | 有研发 标准差 | 有研发企业TFP 标准差更高 | |||
| t值 | p值 | F值 | p值 | |||||
| 1 | -0.022 | 0.202 | 13.873 | 0.000 | 1.022 | 1.113 | 1.187 | 0.000 |
| 2 | -0.013 | 0.206 | 18.685 | 0.000 | 0.778 | 0.842 | 1.172 | 0.000 |
| 3 | -0.010 | 0.196 | 6.957 | 0.000 | 0.904 | 0.964 | 1.138 | 0.010 |
| 4 | -0.028 | 0.511 | 15.170 | 0.000 | 1.033 | 1.314 | 1.620 | 0.000 |
| 5 | -0.092 | 0.592 | 49.966 | 0.000 | 0.982 | 1.446 | 1.396 | 0.000 |
| 6 | -0.019 | 0.225 | 12.187 | 0.000 | 0.955 | 1.168 | 1.496 | 0.000 |
| 7 | -0.022 | 0.296 | 16.205 | 0.000 | 1.024 | 1.201 | 1.375 | 0.000 |
| 8 | -0.040 | 0.240 | 34.844 | 0.000 | 0.610 | 0.799 | 1.717 | 0.000 |
| 9 | -0.064 | 0.305 | 21.316 | 0.000 | 0.903 | 1.119 | 1.536 | 0.000 |
| 10 | -0.116 | 0.423 | 39.845 | 0.000 | 1.065 | 1.475 | 1.918 | 0.000 |
进一步运用Kolmogorov-Smirnov(KS)检验讨论总体上R & D投入对企业生产率的演化是否具有促进作用。作为一种非参数检验方法,KS检验可以确定两组样本量的分布是否显著相同。该检验不依赖均值的位置,具有较强的稳健性。具体地,设GN1(·)和FN0(·)分别是有研发和无研发企业下期生产率的分布函数,N1和N0分别是有无研发的企业数目。双边检验的原假设是两组企业生产率的分布相同,也即:
| ${{H}_{0}}:{{G}_{{{N}_{1}}}}\left( \bar{g}\text{ } \right)-{{F}_{{{N}_{0}}}}\left( \bar{g}\text{ } \right)=0~\forall \bar{g}$ | (13) |
单边检验的原假设是有研发投入的企业比没有研发投入的企业在分布上随机占优,也即:
| ${{H}_{0}}:{{G}_{{{N}_{1}}}}\left( \bar{g}\text{ } \right)\le {{F}_{{{N}_{0}}}}(\bar{g}\text{ })\forall \bar{g}$ | (14) |
检验统计量分别为:
| ${{S}^{1}}=\sqrt{\frac{{{N}_{0}}{{N}_{1}}}{{{N}_{0}}+{{N}_{1}}}}\underset{{\bar{g}}}{\mathop{\max }}\,\left\{ \text{ }\!\!|\!\!\text{ }{{G}_{{{N}_{1}}}}\left( \bar{g}\text{ } \right)-{{F}_{{{N}_{0}}}}\left( \bar{g}\text{ } \right)\text{ }\!\!|\!\!\text{ } \right\}$ | (15) |
| ${{S}^{2}}=\sqrt{\frac{{{N}_{0}}{{N}_{1}}}{{{N}_{0}}+{{N}_{1}}}}\underset{{\bar{g}}}{\mathop{\max }}\,\left\{ \text{ }\!\!|\!\!\text{ }{{G}_{{{N}_{1}}}}\left( \bar{g}\text{ } \right)-{{F}_{{{N}_{0}}}}\left( \bar{g}\text{ } \right)\text{ }\!\!|\!\!\text{ } \right\}$ | (16) |
概率值的计算通过极限分布得到:
| $\begin{align} & P\left( {{S}^{1}}>c \right)=-2\sum _{k=1}^{\infty }{{\left( -1 \right)}^{k}}\exp \left( -2{{k}^{2}}{{c}^{2}} \right) \\ & P\left( {{S}^{2}}>c \right)=\exp (-2{{c}^{2}}) \\ \end{align}$ | (17) |
据表 6左半部分显示,所有行业中有研发和无研发这两类企业的分布显著不同,R & D投入会改变下期生产率的分布。表 6右半部分的检验结果显示,所有行业我们都不能拒绝有研发企业在下期生产率分布上一阶占优的假设,即在生产率的分布上,有R & D投入的企业存在显著的优势。R & D投入对下期企业生产率存在显著的促进作用。
| 行业 | Kolgomorov-Smirnov检验 | |||
| 两分布比较 | 有研发的企业是否一阶占优 | |||
| s1值 | p值 | s2值 | p值 | |
| 1 | 7.317 | 0.000 | 0.021 | 0.999 |
| 2 | 10.183 | 0.000 | 0.015 | 1.000 |
| 3 | 4.111 | 0.000 | 0.045 | 0.996 |
| 4 | 7.476 | 0.000 | 0.014 | 1.000 |
| 5 | 22.310 | 0.000 | 0.033 | 0.998 |
| 6 | 4.505 | 0.000 | 0.044 | 0.996 |
| 7 | 7.152 | 0.000 | 0.011 | 1.000 |
| 8 | 18.354 | 0.000 | 0.534 | 0.566 |
| 9 | 11.470 | 0.000 | 0.039 | 0.997 |
| 10 | 21.520 | 0.000 | 1.037 | 0.116 |
3.R & D投入弹性的异质性
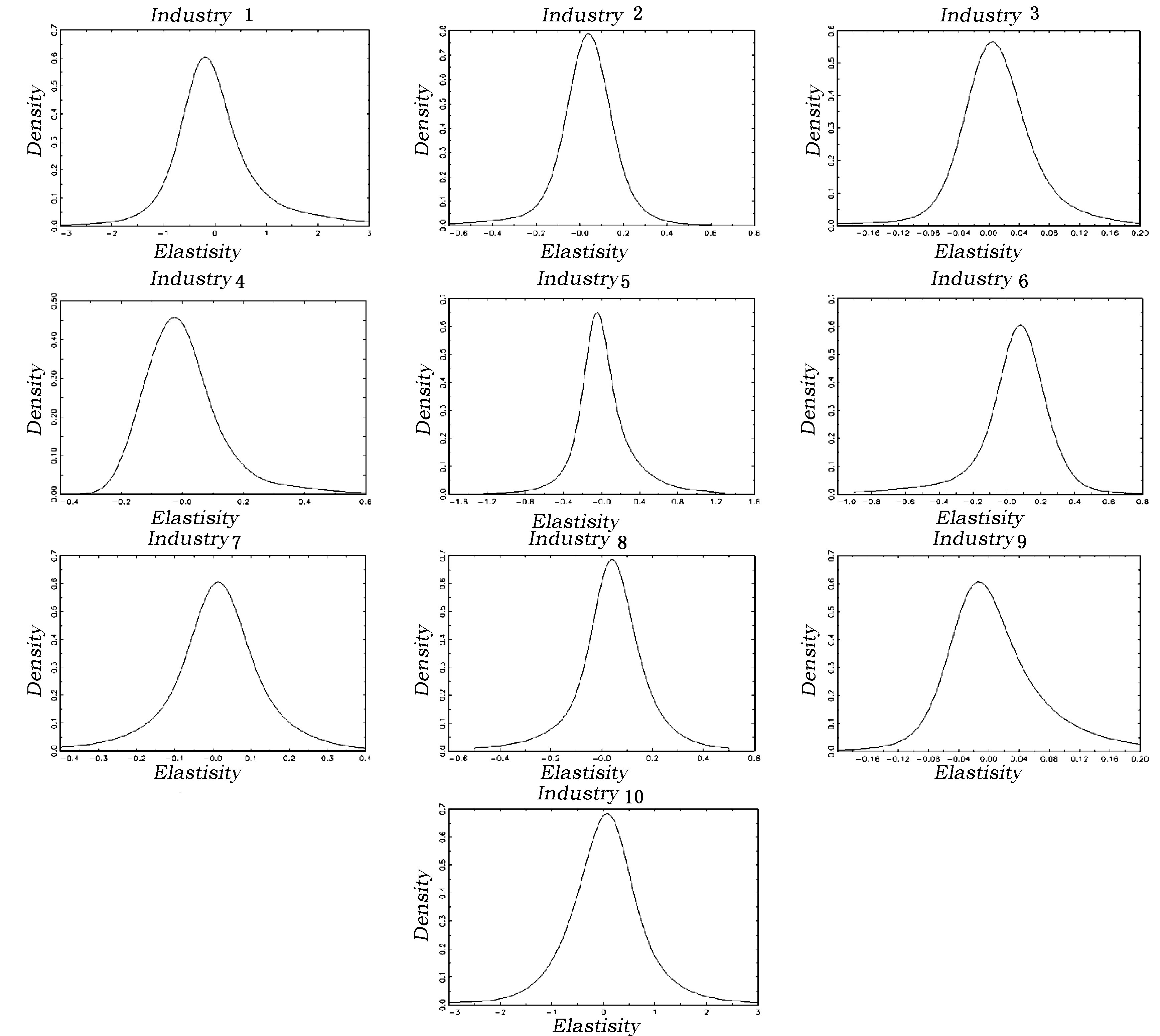
前面的讨论表明,本文估计企业R & D投入回报的理论模型和结构设定是合理的,从总体上看R & D投入对企业生产率的演化具有积极影响。下面我们进一步分析这种影响的企业异质性。估计出了预期生产率函数g(ωit-1,rit-1)后,就可以直接估计R & D投入的边际弹性(只针对有研发投入的企业)。如前文指出,$\frac{{\partial g\left( {{\omega _{it}},{r_{it - 1}}} \right)}}{{\partial {r_{it - 1}}}}$即为t-1期R & D投入对t期预期产出的边际弹性,可以用来度量R & D投入的有效性。表 7和图 1列示了R & D投入边际弹性的分布情况。首先,从均值上看,R & D投入边际弹性与现有文献对中国制造业的估计相差并不大,平均意义上R & D投入的回报很低,甚至为负(如行业10)。其次,R & D投入回报确实具有很强的企业异质性。行业1(食品、饮料和烟草)和行业10(电子)R & D投入边际弹性的方差最大,接近于1。如行业10,R & D投入边际弹性的第25分位值为-0.332,而第75分位值达到0.355。R & D投入边际弹性为负也是合理的,边际上负的回报与全局上R & D投入的正向影响并不矛盾。企业可能会出于先发优势或者R & D投入完整性的考虑,导致短期内R & D投入的边际弹性为负。估计分布与前面的结果也是一致的。例如对于不能拒绝R & D投入线性影响的行业3,图 1中其分布相对而言十分集中,表 7中其方差也最小(只有0.06),即R & D投入边际弹性的企业异质性最小。
| 行业 | q1 | q2 | q3 | q4 | q5 | 简单均值 | 加权均值 | 方差 | 偏度 |
| 1 | -0.714 | -0.371 | -0.140 | 0.279 | 1.043 | 0.037 | 0.035 | 0.888 | 0.199 |
| 2 | -0.093 | -0.002 | 0.039 | 0.074 | 0.140 | 0.012 | 0.039 | 0.218 | -0.125 |
| 3 | -0.027 | -0.006 | 0.003 | 0.026 | 0.063 | 0.007 | 0.013 | 0.060 | 0.060 |
| 4 | -0.125 | -0.074 | -0.016 | 0.047 | 0.145 | 0.004 | 0.004 | 0.124 | 0.158 |
| 5 | -0.257 | -0.114 | -0.034 | 0.121 | 0.370 | 0.016 | 0.002 | 0.320 | 0.158 |
| 6 | -0.192 | 0.010 | 0.067 | 0.143 | 0.227 | 0.033 | 0.045 | 0.235 | -0.145 |
| 7 | -0.131 | -0.032 | 0.011 | 0.058 | 0.141 | 0.005 | -0.011 | 0.147 | -0.043 |
| 8 | -0.126 | -0.010 | 0.037 | 0.101 | 0.182 | 0.029 | 0.030 | 0.183 | -0.042 |
| 9 | -0.047 | -0.025 | -0.007 | 0.036 | 0.098 | 0.012 | 0.026 | 0.078 | 0.241 |
| 10 | -0.845 | -0.332 | 0.065 | 0.355 | 0.854 | -0.041 | 0.034 | 1.066 | -0.09 |
| 注:1.q1、q2、q3、q1和q3分别表示第10分位、第25分位、50分位、75分位和90分位值。2.计算R & D投入边际弹性的加权均值时删除了生产率上下5%,以销售收入为权重。3.偏度定义为:(均值-中位数)/标准差。 | |||||||||
|
| 图 1 预期生产率-R & D投入边际弹性的分布图 |
我们还借鉴文献中的传统做法,对有研发投入的企业样本用滞后一期的R & D投入回归估计的企业生产率,得到平均的R & D投入弹性(本文称为R & D投入平均弹性),如表 8所示。可以看出,平均意义上所有10个行业的R & D投入都对下期实际产出存在显著促进作用。而且,这里估计的R & D投入平均弹性值与国内外现有文献的估计基本一致。这在一定程度上也表明R & D投入的平均回报确实处于一个比较小的区域。
| 行业 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 系数 | 0.023 | 0.020 | 0.020 | 0.049 | 0.056 | 0.024 | 0.029 | 0.025 | 0.029 | 0.044 |
| t值 | 18.37 | 22.13 | 8.52 | 20.60 | 57.21 | 17.11 | 20.99 | 48.72 | 24.44 | 51.00 |
| 注:其他控制变量包括:时间虚拟,地区虚拟以及企业控股状况虚拟。 | ||||||||||
本文的结构估计模型将R & D投入引入企业生产率演化的马尔科夫过程,正式处理R & D投入对企业生产率影响的不确定性、非线性和企业异质性,并同时考虑企业需求的异质性。所有10个行业生产函数和需求函数的参数估计均处在合理的范围内,参数约束检验也表明基本模型的设定是合理的,R & D投入对企业生产率的演化存在显著影响。这说明使用该模型评估R & D投入的产出绩效是可靠的。估计结果表明,R & D投入对其下期生产率的影响确实具有不可忽视的不确定性、非线性和企业异质性。所有行业R & D投入会显著改变行业内企业的生产率分布,进行R & D投入的企业的下期生产率分布显著优于没有进行R & D投入的企业。在充分考虑了影响的不确定性、非线性和企业异质性之后,中国制造业所有行业的R & D投入都能够显著地促进企业生产率发展。
在平均意义上,本文估计的各行业R & D投入平均弹性及R & D投入边际弹性,与使用知识资本模型的国内外文献的估计值并不存在明显差距。然而,所有行业中企业R & D投入的回报确实都具有很强的企业异质性。也正是这种异质性为理解R & D投入回报之谜,即平均意义上R & D投入的回报较低与宏观层面R & D投入对经济增长的重要性共存问题提供了钥匙。即使平均而言R & D投入的回报并不高,但由于其具有高度的企业异质性,一些企业仍然存在较强的激励进行R & D投入;又由于R & D投入取得的新工艺和新产品具有很强的外溢性,部分企业由高额预期回报驱动的R & D投入活动可以成为推动整个经济增长的重要动力。中国经济和社会发展正进入一个全新的时期,人口红利在逐渐消失,资本数量上的扩张也不能再成为经济增长的主要推动力。我们有充分的理由相信,在新阶段R & D投入及由此带来的生产率的改善能够成为推动中国经济持续发展的主要力量。
当然,R & D投入是影响企业长期发展的动态决策。受到数据限制,本文只对四年R & D投入回报进行了估计。随着数据可获得性的增强,本文提出的估计思路可以纳入更为完整的企业动态决策结构,以利用更为丰富的面板信息。
| [1] | 李小平, 朱钟棣. 国际贸易、R & D溢出和生产率增长[J]. 经济研究 , 2006 (2) : 31–43. |
| [2] | 陆国庆. 中国中小板上市公司产业创新的绩效研究[J]. 经济研究 , 2011 (2) : 138–148. |
| [3] | 毛德凤, 李静, 彭飞, 等. 研发投入与企业全要素生产率——基于PSM和GPS的检验[J]. 财经研究 , 2013 (4) : 134–144. |
| [4] | 吴延兵. R & D与生产率——基于中国制造业的实证研究[J]. 经济研究 , 2006 (11) : 60–71. |
| [5] | 尹恒, 杨龙见. 地方财政对本地居民偏好的回应性研究[J]. 中国社会科学 , 2014 (5) : 96–115. |
| [6] | 张海洋. R & D两面性、外资活动与中国工业生产率增长[J]. 经济研究 , 2005 (5) : 107–117. |
| [7] | 周亚虹, 贺小丹, 沈瑶. 中国工业企业自主创新的影响因素和产出绩效研究[J]. 经济研究 , 2012 (5) : 107–119. |
| [8] | 宗庆庆, 周亚虹. 内生情形下企业研发对生产率作用评估[J]. 世界经济文汇 , 2013 (6) : 39–54. |
| [9] | Doraszelski U, Jaumandreu J. R & D and productivity:Estimating endogenous productivity[J]. Review of Economic Studies , 2013, 80 (4) : 1338–1383. DOI:10.1093/restud/rdt011 |
 2016, Vol. 42
2016, Vol. 42




