文章信息
 | 财经研究 2016年42卷第8期 |
- 赵爱栋, 蓝菁, 马贤磊, 许实.
- Zhao Aidong, Lan Jing, Ma Xianlei, Xu Shi.
- 土地价格市场化对中国工业部门要素投入与技术选择的影响
- The Impact of Land Price Marketization on Factor Input and Technology Choice in China's Industrial Sector
- 财经研究, 2016, 42(8): 85-96
- Journal of Finance and Economics, 2016, 42(8): 85-96.
-
文章历史
- 收稿日期:2015-12-07

2016第42卷第8期
2.中国土地勘测规划院,北京 100035
2.China Land Surveying and Planning Institute, Beijing 100035, China
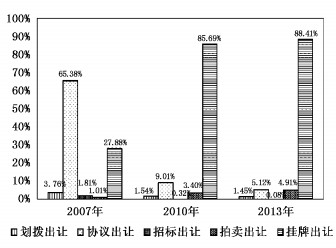
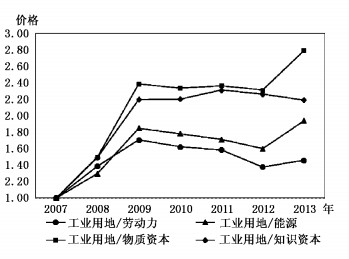
价格市场化是经济转型的关键组成部分,是建立市场经济的必要条件(Roland,2000)。改革开放以来,中国创造性地使用双轨制实现了产品价格的渐进自由化。与产品价格改革顺利进行形成鲜明对比的是生产要素价格改革的相对滞后,其中,土地价格市场化改革进程尤为缓慢。长期的土地价格扭曲为中国经济创造了巨大“土地红利”的同时,也导致经济增长依赖廉价土地的高投入与高消耗(刘守英,2014)。土地市场作为最基本的要素市场,推进土地价格市场化可以成为实现要素优化配置和工业增效升级的重要手段。进入21世纪以来,国家相继出台了一系列法律法规来提高工业用地市场的竞争性和透明度,以充分发挥市场机制在土地价格形成中的决定性作用,扭转了行政划拨和协议出让长期主导中国工业用地资源配置的局面(图 1),土地价值的合理回归推动了工业用地价格上涨,并成为中国要素价格持续上升的重要来源(图 2)。但是土地价格上涨给工业部门带来的影响并未得到学术界足够的重视。
|
| 图 1 中国工业用地出让方式结构(2007-2013年) |
|
| 图 2 工业用地相对价格走势(2007-2013年) |
价格诱致性技术进步假说认为要素相对价格变动不仅能促使企业改变要素投入结构,还能诱致技术创新,短期价格变动会引起要素替代,长期价格改变则会诱致新技术使用(Hayami和Ruttan,1985)。从宏观层面考察,企业根据宏观经济环境中要素相对价格体系实现技术选择与要素投入结构的最优匹配(林毅夫和苏剑,2007),这些微观变化就能够折射出宏观经济增长方式与产业结构调整的未来走向。那么随着国家大力推进工业用地价格市场化,工业用地要素稀缺性在价格形成过程中逐步得到了体现,土地成本上升带来的相对价格效应是否会激励工业部门优化要素投入结构进而集约使用土地,是否会开发或者诱致新的技术来化解成本上升压力,进而取得要素投入产出的最佳效益呢?回答这些问题对评估工业用地价格市场化改革绩效和转变中国工业发展模式具有重要意义。
目前,关于中国土地价格市场化的文献主要集中在市场化改革对土地利用效率、经济增长和收入分配的影响(曲福田,2007;钱忠好,2013;Gao,2014),以及地方政府行为动机研究等方面(石晓平,2005;Li, 2014)。关于要素价格上涨对宏观经济和微观企业层面影响的研究主要集中在能源和劳动力等领域(Popp,2002;Acemoglu和finkelstein,2008;林伯强等,2008;都阳,2013;王班班和齐绍洲,2014)。不过,上述研究还存在改进之处:一是未充分重视土地及其价格在要素投入变动及技术选择中的独特作用。土地财政及地区间“土地引资竞争”逐渐成为中国经济发展模式的重要特征(张五常,2014),而这正是转型期中国土地制度的重要衍生现象。因此忽视土地要素并不能客观反映中国工业化所处阶段和经济增长模式的特征;二是对要素投入变动与技术进步的来源刻画不足。已有研究虽认为要素价格是微观企业一系列经营决策行为的重要信号,但模型构建未能直接体现要素价格变动与要素投入变动和技术进步的直接联系,没有阐释要素相对价格变动对要素投入和技术选择偏向影响的动态演进过程;三是多数实证研究未区分要素相对价格变动的短期效应和长期效应。
针对上述文献的不足,本文基于价格诱致性技术进步假说,构建包含要素相对价格变化、要素投入变动和技术进步的统一的理论分析框架,在此框架下,设定超越对数成本函数模型,从短期和长期的角度分析工业用地相对价格变动对工业部门要素投入和技术选择的影响及其区域异质性。本研究的贡献体现在以下三个方面:第一,从要素投入调整和技术选择倾向的互锁视角,评估了土地价格市场化对工业部门资源配置效率的改进作用,为理解土地价格、工业发展模式和工业转型路径之间的关系提供了独特视角;第二,在中国城市土地制度变迁的背景下,为检验价格诱致性技术进步假说提供了经验基础;第三,区分了要素相对价格变动的短期效应和长期效应,从理论上揭示了短期的要素投入变动和长期技术进步的关系,并进行了实证检验。
二、 理论框架与研究假说价格诱致性技术进步理论将要素价格变化作为一种诱致因子,试图解释要素价格变化如何影响经济体系中的要素投入和技术进步方向,要素相对价格变动诱致企业进行要素替代和增加创新资源投入,最终导致了要素投入变动和生产程序革新或技术进步。
对于单个企业,由于短期技术固定,土地投入在要素投入中的数量变动较小且对价格变动缺乏弹性(Nordhnas,1992;Romer,2001),工业用地相对价格变动的要素投入调整效应不易被察觉。但是,如果将分析视角从微观企业层面上升到宏观工业部门层面,就能避免单一企业短期内土地投入不易变动的局限。区域中处于不同生命周期的企业存在大量的新建、改建、扩建和退出等行为,工业用地价格快速上涨会促使新成立的企业在项目落地时,通过加大土地利用强度(实质为其他要素对土地的替代)或使用土地节约型生产方式,尽量使用较少的土地以减少初始投资成本;而处于成长期的企业在无法有效获得新增用地的情况下,可能倾向于通过厂房改造升级、技术革新或者转移至地价相对低廉的地区等方式来缓解土地对企业发展的制约,这些行为相互叠加将导致短期内区域工业用地投入变动的累积效应比单个企业更为显著。另外,由于土地要素在地区发展战略和产业政策中的定位差异,土地价格上涨使得工业用地价格的杠杆作用更加凸显,这进一步放大了工业用地价格变动的诱致效应。微观企业用地行为的改变反映出工业部门其他要素对土地投入的替代,进而可以窥探区域产业结构调整与产业升级的动向。因此,下文将从区域工业部门角度分析工业用地价格变动的诱致效应。
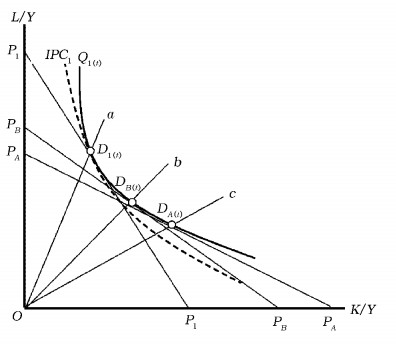
假定有经济发达地区A和经济欠发达地区B,部门生产过程有两种投入要素:一种为工业用地L,另一种为其他投入K(包括资本、劳动力等)。初始t期两地区工业部门生产效率相同,但是土地要素禀赋不同,A地区由于经济发展较早,高强度的土地开发利用使得土地资源禀赋出现衰变退化,工业用地资源较为稀缺,B地区由于经济发展水平落后,生产要素聚集度较低使得工业用地资源充裕。图 3和图 4中,横坐标和纵坐标分别代表每单位产出中土地L与其他要素K的投入比例,Q是等产量曲线,代表技术水平不变情况下生产单位产出的所有投入要素组合,射线a、b和c表示每一单位产出中工业用地L和其他要素K的投入比例,即要素投入组合,创新可能性曲线IPC是所有可供选择的等产量曲线的包络线,代表在不同技术水平下生产单位产出的最有效率的要素组合点。要素价格不仅能促使工业部门选择最优的要素投入组合(相对价格线与等生产线的切点),也能促使其选择最佳的生产技术(相对价格线与IPC的切点)。
|
| 图 3 工业用地价格与短期要素投入变动 |
|
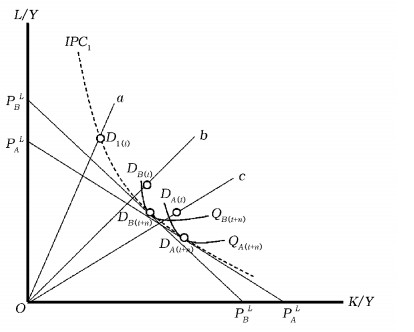
| 图 4 工业用地价格与长期技术选择 |
如图 3所示,初始t期在长期技术水平IPC1和要素相对价格P1P1下,A、B两地部门最优生产决策点均为D1(t)。随着工业用地价格市场化改革,工业用地价格变得相对昂贵,但是两地区工业价格受到的冲击存在差异,A地被人为压低的工业用地价格逐渐回归以反映其土地资源的稀缺性,要素相对价格线由P1P1旋转为PAPA,B地工业用地价格反映了其相对充足的土地资源优势,要素相对价格线由P1P1旋转为PBPB。土地成本上升会促使工业部门在生产技术或生产程序许可的范围内重新调整工业用地与其他要素的组合比例。在短期技术水平不变和新的要素价格体系下,A、B两地最优生产决策点将沿着等产量线Q1(t)移动分别变为DA(t)和DB(t),要素投入组合的变动表示短期内生产过程中其他要素对土地的替代。但实际上,这种调整还受到要素间替代关系及弹性值大小的影响,要素投入变动取决于工业用地与其他要素替代的可能性。对于A地来说,土地资源稀缺对经济发展造成约束,面对工业用地价格上涨更可能会诱致部门内部其他要素对工业用地的替代。B地经济发展面临的土地资源约束较小,工业用地价格的扰动能在多大程度上产生工业用地替代效应则不易确定。基于此,提出本文的研究假说一:
H1:短期内,工业用地相对价格上升会诱致工业部门使用其他要素替代工业用地,工业用地相对投入比例会出现下降,这种短期诱致替代效应在发达地区更加显著。
(二) 工业用地价格变动与长期技术选择长期内,工业用地长期价格PL进一步改变,暂时性的要素投入变动在短期生产技术既定和要素间替代弹性存在限制的情况下可能不是最优。如图 3所示,A、B两地短期的最优生产决策点DA(t)和DB(t)均偏离了长期技术曲线IPC1的轨迹,现有的要素投入变动并没有完全反映潜在的可利用技术,还有进一步优化的空间。因此,要素相对价格的持续变化会驱使部门进行技术革新,技术进步的直接结果就是部门等生产量曲线向IPC1所代表的长期技术前沿面靠近,此时工业部门可以使用更少的要素投入生产单位产出,并使得继续调整要素间替代弹性成为可能。由于资源禀赋不同,A、B两地的长期技术选择会出现分化。A地面对土地资源劣势可能促使一些成本敏感的行业进行区域转移,并通过增加R & D投入等创造性资源来改变现有生产技术或开发更富效率的生产程序,发展土地集约型工业,从而进一步减少对土地要素的依赖,最终A地的等产量线由图 3中的Q1(t)内移至图 4中的QA(t+n),这时A地工业部门可以用更少的土地投入生产单位产出,最优生产点变为DA(t+n),DA(t+n)具备长期技术有效性。但是长期内B地受到的土地成本上涨冲击并没有A地区大,其工业发展的主要思路依然是有效组合具有比较优势的土地等生产要素,以差异化战略参与区域竞争,因此B地等产量线仅移动至DB(t+n),长期内最优生产点由DB(t)变为DB(t+n)。总体来看,在工业用地相对价格提高的情况下,A、B两地工业部门在利用其他要素K替代工业用地L的同时,不同程度地提高了要素使用效率。D1(t)到DA(t+n)(或DB(t+n))的转变代表了要素相对价格变动诱致的要素投入变动和土地节约型技术进步。基于此,提出本文的研究假说二:
H2:长期内,工业用地相对价格上升会诱致工业部门采用土地节约型技术进步化解成本上升压力,这种长期技术创新诱致效应在发达地区更加显著。
三、 模型设定与估计方法 (一) 包含要素价格的超越对数成本函数模型本文假设追求利润最大化的企业以期望的未来市场信息做出决策,则工业部门中代表性企业的成本函数为:
| $C=G\left({y, p, \rho, X, T} \right)$ | (1) |
(1)式中G(·)为长期规模报酬不变的成本函数,并且对于要素价格是线性齐次、非递减的凹函数,对于产出y是非递减的。y代表产出,P是要素X的当前市场价格,ρ是依赖于要素当前和过去价格的要素长期价格。X为投入要素,包含劳动力W、能源E、工业用地L、物质资本Kw和知识资本Ke。T代表企业的技术状态并可分为两部分:第一部分表示与企业R & D投入和要素价格变动无关的外生技术,即时间趋势变量t;第二部分是与要素价格变动相关的企业内生技术,本文称之为价格诱致性技术进步。
为方便刻画要素替代和技术进步,成本函数C又可以进一步表示为包含劳动力、工业用地及产出等的超越对数成本函数形式(Jorgensen,2007;樊茂清等,2012):
| $\begin{array}{l} {C_t}={\alpha _0} + {\alpha _y}{\rm{ln}}{y_t} + \sum\limits_{i=1}^5 {{\beta _i}{\rm{ln}}{P_{it}}} + {\alpha _t}t + \frac{1}{2}\left({{\gamma _{yy}}{\rm{l}}{{\rm{n}}^{\rm{2}}}{y_t} + \sum\limits_{i=1}^5 {\sum\limits_{j=1}^5 {{\beta _{ij}}{\rm{ln}}{P_{it}}{\rm{ln}}{P_{jt}} + {\alpha _{tt}}{t^2}} } } \right)\\ \; \;\; \;\; \;\; + \sum\limits_{i=1}^5 {{\beta _{it}}{\rm{ln}}{P_{it}}t} + \sum\limits_{i=1}^5 {{\beta _{iy}}{\rm{ln}}{P_{it}}{\rm{ln}}{y_t}} + {\gamma _{yt}}t{\rm{ln}}{y_t} \end{array}$ | (2) |
(2)式中,i,j=W,E,L,Kw,Ke。(1)式中的外生技术进步在(2)式中表示为时间趋势t,而价格诱致性技术进步的发生涉及企业对未来要素价格变化的预期,只有预期要素相对价格在较长一段时期内持续失衡时,企业才会加大投入进行生产技术创新。价格诱致的技术动态调整存在滞后期,这种诱致机制的发生依赖于R & D投入等科技创新资源对要素长期价格的响应。因此价格诱致机制可以看成要素长期价格ρ的某种函数形式。参照Esposti和Pierani(2008)等人的研究,本文根据考伊克几何分布滞后模型建立价格诱致的动态过程,即:
| ${\rho _{it}}=\lambda {p_{i, t-1}} + {\lambda ^2}{p_{i, t-2}} +... + {\lambda ^\tau }{p_{i, t-\tau-1}}=\sum\limits_{\tau=0}^\infty {{\lambda ^\tau }} {p_{i, t-\tau-1}}=\frac{1}{{1-\lambda }}{p_{i, t-1}}\left({1 < \lambda < 1} \right)$ | (3) |
(3)式隐含着当期价格的诱致效应从t-1期开始随着滞后期的增加而几何衰减,而λ决定了滞后衰减的速度,λ越接近0,衰减速度越快,λ越大则表示价格的诱致效应越大。
由(2)式,根据Shepard引理可得工业部门要素投入份额函数Si:
| ${S_{it}}{\rm{=}}{X_{it}} \cdot \frac{{{P_{it}}}}{C}{\rm{=}}\frac{{\partial {\rm{ln}}C}}{{\partial {\rm{ln}}{P_{it}}}}=\frac{{\partial C}}{{\partial {P_{it}}}} \cdot \frac{{{P_{it}}}}{C}={\beta _i} + \sum\limits_{j=1}^5 {{\beta _{ij}}} {\rm{ln}}{P_{jt}} + t{\beta _{it}} + {\beta _{iy}}{\rm{ln}}{y_t}$ | (4) |
为了更好地识别要素需求在要素价格冲击下的动态调整及要素价格的滞后效应,(3)式经过Koyck变换后可将(4)式改写成下列动态要素投入份额方程:
| ${S_{it}}=\frac{{\partial {\rm{ln}}C}}{{\partial {\rm{ln}}{\rho _{it}}}}=\lambda {S_{it-1}} + (1-\lambda){\beta _i} + \sum\limits_{j=1}^5 {{\beta _{ij}}{\rm{ln}}{P_{jt}}} + {\beta _{it}}t + {\beta _{iy}}{\rm{ln}}{y_t}$ | (5) |
此外,为了满足超越对数成本函数齐次性、对称性、长期规模报酬不变等假设,有如下模型参数约束条件:
| $\sum\limits_i {{\beta _i}}=1, \quad \sum\limits_i {{\beta _{iy}}}=0, \quad {\beta _{ij}}={\beta _{ji}}, \quad \sum\limits_i {{\beta _{ij}}}=0, \quad {\beta _{ji}}={\beta _{ij}}$ |
1.要素替代与要素投入变动方程。要素投入的变动是工业部门在要素相对价格变动的情况下通过要素替代等一系列行为实现的,而Morishima替代弹性可以较准确地估计两种要素投入比率对相对价格的反应程度(黄光晓,2011)。因此,本文用Morishima替代弹性来衡量生产中任意两种生产投入要素的替代程度,公式为:
| ${\sigma _{ij}}=\frac{{\partial {\rm{ln}}({x_i}/{x_j})}}{{\partial {\rm{ln}}{p_j}}}=\frac{{\partial {\rm{ln}}{x_i}}}{{\partial {\rm{ln}}{p_j}}}-\frac{{\partial {\rm{ln}}{x_j}}}{{\partial {\rm{ln}}{p_j}}}={\varepsilon _{ij}}-{\varepsilon _{jj}}$ | (6) |
式(6)说明Morishima替代弹性是由交叉价格弹性(εij)和自价格弹性(εjj)决定的,根据要素投入、要素份额与要素价格的关系,可得:
| ${\varepsilon _{ij}}=\frac{{\partial ln{x_i}}}{{\partial ln{p_j}}}{\rm{=}}\frac{{\partial ln{S_i}}}{{\partial ln{p_j}}} + \frac{{\partial lnC}}{{\partial ln{p_j}}}-\frac{{\partial ln{p_i}}}{{\partial ln{p_j}}}=\frac{{{\beta _{ij}}}}{{{S_i}}} + {S_j}, 如果i \ne j, 则{\varepsilon _{jj}}=\frac{{\partial ln{x_j}}}{{\partial ln{p_j}}}=\frac{{{\beta _{jj}}}}{{{S_j}}} + {S_j}-1$ | (7) |
由于要素自价格弹性εjj < 0,根据式(6)和式(7)可知,当σij>0时,如果εij>0,则要素i与要素j呈替代关系;当σij < 0时,如果εij < 0,则二者之间呈互补关系,但是当εij>0时,二者之间的替代关系则具有不确定性。
2.要素相对价格变动与技术选择方程。要素相对价格变动不仅导致了要素投入变动,长期也会对部门技术选择产生影响,沿用Peeters和Surry(2000)、Esposti和Pierani(2008)等的做法,定义诱致性技术进步为随着长期价格变动部门生产成本减少的幅度,工业用地价格变动诱致的技术进步可以表示为:
| ${\gamma _{cl}}=\partial {\rm{ln}}C/\partial {\rm{ln}}{\rho _L}=\partial {\rm{ln}}C/(\partial {\rm{ln}}{p_L}/(1-\lambda))=(\partial {\rm{ln}}C/\partial {\rm{ln}}{p_L})/(1-\lambda)$ | (8) |
当γCl < 0,说明工业用地价格上涨在长期内确实诱致部门内部开发或使用新技术来化解成本上升压力。进一步,结合要素投入份额函数(4),参考Binswanger(1974)、Celikkol(1999)等人关于价格变化诱致的技术进步对要素投入决策的测算方法,诱致性技术进步对要素投入产生的效应表示为:
| ${\psi _{iL}}=\partial {s_i}/\partial {\rm{ln}}{\rho _L}=\partial {s_i}/(\partial {\rm{ln}}{p_L}/(1-\lambda))=({s_i}({\varepsilon _{iL}}-{\gamma _{Cl}}))/(1-\lambda)$ | (9) |
(9)式中,si表示第i要素在总成本C中所占的份额,εil为工业用地与第i种投入要素的替代弹性,i=W,E,Kw,Ke。ψil < 0(或ψil>0)表示工业用地价格上涨导致i要素投入份额减少(增加),说明工业用地价格上涨诱致了i要素节约型(使用型)技术进步。
另外,定义外生技术进步为随着时间变化部门生产成本减少的幅度:εct=∂lnCt/∂t。外生技术进步导致的要素投入变动效应可以表示为:
| ${B_{it}}=\partial {s_i}/\partial t={s_i}({\varepsilon _{it}}-{\varepsilon _{ct}})$ | (10) |
其中,εit=∂lnxi/∂t外生技术进步更倾向于使用(Bit>0)或节约(Bit < 0)i要素投入取决于其投入变动幅度是否大于或者小于成本减少的速度。
(三) 估计方法考虑到不同的要素需求方程的扰动项之间可能存在相关性,加之横截面数据中经常出现的异方差问题,本文根据方程(5),将各要素份额方程构成一个联立方程组,并去掉知识资本投入份额方程,采用似不相关回归方法(SUR)对方程组模型进行估计(樊茂清等,2012;王班班和齐绍洲,2014)。本文构造的联立方程组模型如下:
| $\left\{ \begin{array}{l} {S_W}{\rm{=}}{\lambda _W}{S_{W, t-1}} + \beta _W^* + {\beta _{WW}}{\rm{ln}}P_W^* + {\beta _{WE}}{\rm{ln}}P_E^* + {\beta _{wL}}{\rm{ln}}P_L^*\\ \; \;\; \;\; \;\; + {\beta _{wKw}}{\rm{ln}}P_{{K_w}}^* + {\beta _{wt}}t + {\beta _{wy}}{\rm{ln}}{y_t} + {\varepsilon _W}\\ {S_E}{\rm{=}}{\lambda _E}{S_{E, t-1}} + \beta _E^* + {\beta _{EE}}\ln P_E^* + {\beta _{EW}}{\rm{ln}}P_W^* + {\beta _{EL}}{\rm{ln}}P_L^*\\ \; \;\; \;\; \;\; + {\beta _{EK{\rm{w}}}}{\rm{ln}}P_{{K_W}}^* + {\beta _{Et}}t + {\beta _{Ey}}{\rm{ln}}{y_t} + {\varepsilon _E}\\ {S_L}{\rm{=}}{\lambda _L}{S_{L, t-1}} + \beta _L^* + {\beta _{LL}}{\rm{ln}}P_L^* + {\beta _{LW}}{\rm{ln}}P_W^* + {\beta _{LE}}{\rm{ln}}P_E^*\\ \; \;\; \;\; + {\beta _{LKw}}{\rm{ln}}P_{Kw}^* + {\beta _{Lt}}t + {\beta _{Ly}}{\rm{ln}}{y_t} + {\varepsilon _L}\\ {S_K}_w{\rm{=}}{\lambda _{Kw}}{S_K}_{w, t-1} + \beta _{K{\rm{w}}}^* + {\beta _{KwKw}}{\rm{ln}}P_{Kw}^* + {\beta _{KwW}}\ln P_W^*\\ \; \;\; \;\; \; + {\beta _{KwL}}\ln P_L^* + {\beta _{KwE}}\ln P_E^* + {\beta _{Kwt}}t + {\beta _{Kwy}}{\rm{ln}}{y_t} + {\varepsilon _{Kw}} \end{array} \right.$ | (11) |
式(11)中,lnPj*=lnPj/lnPke,即各要素与知识资本的相对价格,βj*=(1-λ)βi。由于方程组内部的跨方程参数约束,回归时对方程组进行了参数约束。
四、 数据来源与变量说明本文选取2007-2013年中国大陆除西藏外30个省(市、区)工业部门投入产出面板数据进行实证分析,为了便于成本加和和计算要素份额,所有投入要素价格均为指数形式,以2007年为基年并设置为1。其余变量均为2007年不变价。变量及数据说明如下:
1.产出(y)。选用工业总产值衡量。
2.物质资本投入(Kw)和资本价格(PKw)。采用工业行业资本存量作为资本投入,资本存量使用永续盘存法计算(张军,2004)。关于资本价格,一般认为资本租赁价格可作为资本真实使用成本,本文根据Jorgenson(1991)提出的估计方法:pkw=Ckw=qt(rt+δt)-(qt-qt-1)计算。其中,qt为t期资产的市场购置价格,r为净收益率,δ为资本折旧率。本文使用三年期实际贷款利率测度r,资产的市场购置价格q使用固定资产投资价格指数来代替。
3.知识资本投入(Ke)和价格(PKe)。使用“各地区规模以上工业企业R & D经费内部支出”作为知识资本投入(Popp,2002;Wing,2006),并设定R & D价格指数=0.5×(消费价格指数+固定资产投资价格指数)作为知识资本价格(白俊红,2009)。
4.劳动力投入(W)和劳动力价格(PW)。采用“工业行业城镇单位就业人员数”衡量劳动力投入W。劳动力价格PW以“工业行业城镇单位就业人员平均工资”来代替。
5.能源投入(E)和能源价格(PE)。使用扣除了“用作原料、材料”部分的“工业行业终端能源消费量(标准量)”作为工业部门能源投入。鉴于分省的能源价格PE不能直接获得,参考鲁成军和周端明(2008)的做法,采用分省“燃料、动力购进指数”代替。
6.工业用地投入(L)和工业用地价格(PL)。省级工业用地投入选用建成区工业用地面积,工业用地价格使用单位面积工业用地出让价格衡量。
以上变量均来自历年《中国统计年鉴》、《中国科技统计年鉴》、《中国能源统计年鉴》和《中国城市建设统计年鉴》等。限于篇幅,相关变量的描述性统计不再展示。
五、 实证结果及分析 (一) 估计结果表 1汇报了联立方程组的参数估计结果。LM检验结果在0.01%的水平上拒绝了“各方程的扰动项无同期相关”的原假设,可以推断本文使用似不相关回归法是合理的。从调整后的R2来看,各回归方程的拟合程度均较好,估计的Koyck参数λ均在0.01%的水平上显著为正且不等于0,表明几何分布滞后模型能够较好地反映要素相对价格变动的诱致效应。另外,本文对联立方程组模型估计结果进行了经济学意义上的检验,除了已经设定的齐次性约束,还需满足以下条件:一是非递减性要求成本函数是关于任意要素价格的非递减函数,所有模型中,βi>0保证了成本函数对要素价格非递减;二是给定产出水平,成本函数是任意要素价格的凹函数,即要素的自价格弹性为负。经过计算,劳动力、能源、物质资本、知识资本要素的自价格弹性均为负值(见表 2),而工业用地自价格弹性与经济理论相反,为正值,本文将在下文具体讨论。
| 工业用地需求SL | 劳动力需求SW | 能源需求SE | 物质资本需求SKw | ||||
| 变量 | 估计值 | 变量 | 估计值 | 变量 | 估计值 | 变量 | 估计值 |
| λL | 0.338*** (3.89) |
λW | 0.677*** (5.93) |
λE | 0.365*** (4.99) |
λKw | 0.383*** (5.97) |
| βL | 0.067*** (3.04) |
βW | 0.021*** (2.84) |
βE | 0.910*** (17.78) |
βKw | 0.003 (0.06) |
| βLL | 0.062*** (10.45) |
βWW | 0.004 (0.93) |
βEE | 0.170*** (8.60) |
βKwKw | 0.147*** (4.84) |
| βLE | -0.045*** (-6.10) |
βWE | -0.007** (-2.26) |
βEW | -0.007** (-2.26) |
βKwW | 0.013* (1.77) |
| βLW | -0.002 (-1.13) |
βWL | -0.002 (-1.13) |
βEL | -0.045*** (-6.10) |
βKwE | -0.111*** (-6.47) |
| βLKw | -0.026*** (-3.31) |
βWKw | 0.011* (1.77) |
βEKw | -0.111*** (-6.47) |
βKwL | -0.026*** (-3.31) |
| βLKe | 0.012** (1.97) |
βWKe | -0.007** (-2.26) |
βEKe | -0.007 (-0.80) |
βKwKe | -0.024 (-0.89) |
| βLt | -0.001 (-0.58) |
βWt | 0.001 (1.14) |
βEt | -0.008** (-2.46) |
βKwt | 0.010*** (3.24) |
| βLy | -0.004 (-1.46) |
βWy | -0.002** (-2.57) |
βEy | -0.042*** (-6.74) |
βKwy | 0.033*** (5.89) |
| R2 | 0.504 | R2 | 0.363 | R2 | 0.445 | R2 | 0.423 |
| chi2 | 229.540 | chi2 | 58.090 | chi2 | 199.550 | chi2 | 198.210 |
| P值 | 0.000 | P值 | 0.000 | P值 | 0.000 | P值 | 0.000 |
| 样本数量 | 30/210 | ||||||
| Breusch-Pagan test :chi2(6)=225.487*** | |||||||
| 注:*、**、***分别表示在10%、5%和1%的水平下显著,括号内为Z统计量,下同。 | |||||||
从全国层面看,2007-2013年间,工业用地自价格弹性均值为正,同时工业用地与劳动力、能源和物质资本的Morishima弹性均值为负,理论上表现出互补关系(表 2)。该发现表明工业用地相对价格的上升不仅没有起到抑制工业部门土地需求的作用,反而诱致工业用地相对投入比例出现上升。这可能与中国工业发展阶段以及工业用地价格市场化改革的特征密切相关,表现在:(1)持续高速的经济增长一定程度上造成了工业用地的需求刚性。当前,中国大部分地区仍处在工业化阶段,旺盛的用地需求与土地资源短缺的矛盾一定程度上限制了价格效应的发挥;(2)土地价格长期扭曲,仍然没有完全市场化。长期以来,中国工业用地价格被各种协议价格或无偿划拨等行政行为所扭曲(陶然等,2009),近年来工业用地价格市场化改革虽已有显著成效,但地方政府在工业用地出让市场中仍具有相当的垄断能力和强烈的干预欲望(陶然等,2010)。赵爱栋等(2016)的研究发现,2007-2013年中国工业用地出让价格加权溢价率仅为1.03,工业用地出让价格长期徘徊在工业用地成本价格附近。
| 自价格弹性 | Morishima弹性 | ||||
| εLL | σWL | σEL | σKwL | σKeL | |
| 全国 | 0.046 (0.50) |
-0.156 (-0.97) |
-0.060 (-0.61) |
-0.066 (-0.64) |
1.773* (1.79) |
| 东部 | -0.149** (-2.02) |
0.100(0.80) | 0.147* (1.86) |
0.160* (1.86) |
1.210** (2.14) |
| 中部 | 0.284 (2.40) |
-0.420** (-2.31) |
-0.309** (-2.55) |
-0.300** (-2.44) |
2.310* (1.62) |
| 西部 | 0.188 (1.73) |
-0.370* (-1.71) |
-0.203* (-1.79) |
-0.230** (-1.93) |
3.960* (1.75) |
| 注:限于篇幅,表中只列出了与工业用地有关的价格弹性。L=工业用地,W=劳动力,E=能源,KW=物质资本,Ke=知识资本,Y=产出,下同。 | |||||
从区域差异来看,东部地区工业用地自价格弹性均值显著为负,同时工业用地与劳动力、能源、物质资本和知识资本的平均Morishima弹性均为正值,说明东部地区工业用地与劳动力、能源、物质资本和知识资本表现出替代关系。这意味着随着工业用地相对价格上升,将会诱致东部地区工业部门使用其他要素替代工业用地投入。中西部地区要素弹性估计结果与全国层面相似。在工业用地价格冲击下,东部与中西部地区Morishima替代弹性表现出截然相反的结果,原因主要在于东部地区在工业转型升级过程中面临着比中西部更为严峻的土地稀缺困境,工业用地的绝对价格和相对价格涨幅也远高于中西部地区。工业用地价格快速上涨更能激励东部地区调整要素组合,节约使用相对稀缺的土地要素,并进行技术革新。
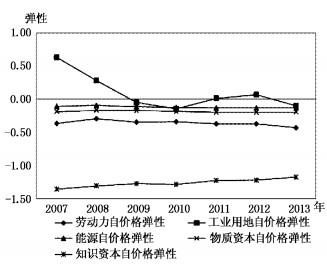
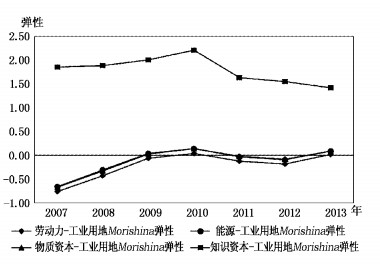
从时间维度变化来看,工业用地自价格弹性呈现出明显的下降趋势,由2007年的0.63下降至2013年的-0.1,这表明,虽然从均值来看,工业用地相对价格上升并没有诱致工业部门节约相对稀缺的土地要素,但是随着工业用地价格市场化的推进,土地价格上升对工业用地需求的抑制作用逐渐显现。工业用地与劳动力、能源、物质资本的Morishima弹性值则呈上升趋势,在2010和2013年甚至两度由互补关系转为替代关系(见图 4和图 5)。工业用地与知识资本的Morishima弹性值表明两者间具有很强的替代关系。
|
| 图 4 工业用地与其他要素的自价格弹性 |
|
| 图 5 工业用地与其他要素的Morishima替代弹性 |
最后,从图 4还可以看出,知识资本自价格弹性绝对值大于1,表明工业部门对R & D投入的价格变动较为敏感。可能的解释是,由于中国土地、能源等要素价格长期扭曲使得部门倾向于密集使用有形要素,而缺少动力投资于自主创新(张杰,2011)。
总体来看,随着工业用地相对价格的上升,东部地区出现显著的工业用地替代效应,工业用地相对劳动力、能源和物质资本的投入比例出现下降,而在全国层面和中西部则没有诱致工业部门使用其他要素替代工业用地,说明经济越发达的地区,要素相对价格变动的短期诱致替代效应越显著。该结论支持了研究假说1。
(三) 要素相对价格变动的长期技术选择效应表 3显示了不同来源的长期技术进步对要素投入的偏向性影响。要素投入偏向显示,价格诱致性技术进步偏向于节约土地,但未获得显著性支持,说明工业用地的快速上涨诱致的工业用地节约型技术进步特征尚不明显。能源和物质资本节约型技术特征与知识资本使用型技术特征进一步验证了工业用地与能源和物质资本间的互补关系以及与知识资本间的替代关系,工业用地价格上涨诱致的长期技术创新效应进一步强化了短期的替代效应。这一发现启示我们应充分重视土地价格市场化对过度投资的抑制作用和对企业技术创新的激励效应,土地作为经济发展最基本的投入要素,对土地要素的合理配置将直接影响其承载的要素投入组合和技术选择,推进土地价格市场化可以成为撬动中国工业增长模式转变的重要杠杆。
| 2007-2013年 | 工业用地L | 劳动力W | 能源E | 物质资本Kw | 知识资本Ke | |
| 诱致性技术进步ψiL | 全国 | -0.001 (-0.16) |
-0.002 (-1.01) |
-0.046*** (-5.75) |
-0.027*** (-3.31) |
0.011* (1.84) |
| 东部 | -0.021*** (-3.00) |
0.001(0.23) | -0.045*** (-4.22) |
-0.076*** (-3.91) |
0.027* (1.88) |
|
| 中部 | 0.013** (2.02) |
-0.009** (-2.04) |
-0.015 (-0.41) |
0.030 (-0.93) |
0.015 (1.12) |
|
| 西部 | 0.008 (1.24) |
-0.003 (-0.77) |
-0.048*** (-3.34) |
-0.029** (-2.52) |
0.012 (1.35) |
|
| 外生性技术进步BiL | 全国 | -0.001 (-0.58) |
0.003 (1.63) |
-0.008** (-2.46) |
0.098*** (60.91) |
0.001 (0.63) |
从区域差异来看,随着工业用地相对价格的上升,东部地区表现出显著的工业用地节约型技术进步特征,中部地区诱致性技术进步则偏向于使用工业用地,西部地区工业用地使用型技术进步特征未得到显著支持。东部地区在经济转型和土地资源短缺的双重压力下,除了要素相对价格体系受到的冲击更为显著外,工业用地市场发育程度和价值显著程度也领先于中西部地区(赵爱栋等,2016),工业用地市场价值的逐步回归使得企业在建厂或者扩大规模时需要充分考虑要素投入组合,倒逼企业依靠增加R & D等科技投入来提升自身竞争力,进而通过发展土地集约型技术来摆脱土地资源约束。而中西部地区目前正处在加速工业化进程阶段,以资源消耗型为主的产业结构催生了旺盛的增量用地需求,加之工业用地价格整体较低,土地价格的上涨对企业的长期决策没有产生明显的导向作用,因此,中西部地区工业用地相对价格变动没有诱致土地节约型技术进步的发生。
另外,本文也观察到2007-2013年,中国工业部门经历了较为显著的外生性技术进步,εct值达到了-0.304(P值-1.95),远远大于价格诱致性技术进步。外生性技术进步要素投入偏向显示,资本使用型技术进步主导了工业部门技术进步,这表明金融危机以来,中国工业部门进一步偏向了资本密集型的增长路径,资本深化程度不断提高,而研究期内,工业部门增长模式并没有出现明显的土地节约型的技术选择倾向。
总体来看,工业用地相对价格上升会诱致工业部门采用土地节约型技术进步化解成本上升压力,虽然这种长期技术创新诱致效应在全国层面尚不明显,但是在东部地区则得到了显著支持,这说明经济越发达的地区,要素相对价格变动诱致的长期技术创新效应越显著。该发现支持了研究假说2。
六、 结论和启示实证结果表明:短期内,要素相对价格变动的诱致替代效应仅在东部地区成立,表现为东部地区工业用地相对价格上升不仅能够起到抑制工业用地需求的作用,而且还诱致工业部门使用非土地要素替代工业用地投入;但在全国层面和中西部地区,工业用地相对价格的上升并没有诱致工业部门节约相对稀缺的土地要素。长期内,工业用地相对价格上升诱致的土地节约型技术仅在东部地区成立,全国层面和中西部地区都不显著。
价格市场化改革能够带来资源配置效率的改进,但是中国土地价格扭曲仍未有效消除以及工业用地刚性需求等,均导致了工业用地价格市场化改革未能充分发挥预期效果。因此,为了优化工业要素投入结构,加快推进中国工业转型升级,本文从工业用地要素角度提出以下政策建议:第一,继续深化工业用地价格市场化改革,建立和完善反映资源稀缺程度的工业用地价格形成机制,同时合理调控工业用地供需结构,充分发挥工业用地价格的杠杆作用来促进产业优胜劣汰;第二,有效遏制囤地、炒地和工业用地闲置浪费等行为。警惕企业脱离实体经济进入工业用地市场投机炒作,强化行政手段对囤地、炒地、土地闲置等行为的打击,实现工业用地资源的有效配置;第三,鉴于目前中国工业用地仍然具有较强的需求刚性,因此通过提高工业用地价格来抑制旺盛的工业用地需求可能效果甚微,要实现土地节约集约利用,走土地集约型发展模式最终需要调整产业结构和实现产业升级。
| [1] | 林毅夫, 苏剑. 论我国经济增长方式的转换[J].管理世界,2007(11):5–13. |
| [2] | 鲁成军, 周端明. 中国工业部门的能源替代研究——基于对ALLEN替代弹性模型的修正[J].数量经济技术经济研究,2008(5):30–42. |
| [3] | 樊茂清, 郑海涛, 孙琳琳, 等. 能源价格、技术变化和信息化投资对部门能源强度的影响[J].世界经济,2012(5):22–45. |
| [4] | 王班班, 齐绍洲. 有偏技术进步、要素替代与中国工业能源强度[J].经济研究,2014(2):115–127. |
| [5] | 赵爱栋, 马贤磊, 曲福田, 等. 基于资源价值显化视角的中国工业用地市场发育水平及其影响因素[J].资源科学,2016a(2):217–227. |
| [6] | 赵爱栋, 马贤磊, 曲福田. 市场化改革能提高中国工业用地利用效率吗?[J].中国人口·资源与环境,2016b(3):118–126. |
| [7] | Acemoglu D, Finkelstein A. Input and technology choices in regulated industries:Evidence from the health care sector[J].Journal of Political Economy,2008,116(5): 837–880. |
| [8] | Esposti R, Pierani P. Price-induced technical progress in Italian agriculture[J].Review of Agricultural and Environmental Studies,2008,89(4): 5–28. |
| [9] | Peeters L, Surry Y. Incorporating price-induced innovation in a symmetric generalised McFadden cost function with several outputs[J].Journal of Productivity Analysis,2000,14(1): 53–70. |
| [10] | RolandG. Transition and economics:Politics, markets and firms[M]. Cambridge: MIT Press, 2000 . |
| [11] | Wing S I. Representing induced technological change in models for climate policy analysis[J].Energy Economics,2006,28(5-6): 539–562. |
 2016, Vol. 42
2016, Vol. 42



