文章信息
- 景鹏, 胡秋明
- Jing Peng, Hu Qiuming
- 生育政策调整、退休年龄延迟与城镇职工基本养老保险最优缴费率
- Fertility Policy Adjustment, Retirement Age Extension and Optimal Contribution Rate of State Basic Pension Scheme for Urban Employees
- 财经研究, 2016, 42(4): 26-37
- Journal of Finance and Economics, 2016, 42(4): 26-37.
-
文章历史
- 收稿日期:2015-07-15
一、引言与文献综述
伴随人口出生率的迅速下降和人口预期寿命的不断延长,中国人口年龄结构已然发生了深刻变化,人口老龄化问题日益严重。人口老龄化给"未富先老"的中国经济社会发展带来了诸多挑战,尤其使背负着庞大隐性债务的城镇职工基本养老保险制度的偿付能力持续弱化。为了应对人口老龄化对基本养老保险制度的冲击,延迟退休年龄、调整计划生育政策和提高社会统筹缴费率等参量式改革方案为学界所提倡。
众多国外学者(Cremer和Pestieau,2003;Lacomba和Lagos,2010)均认为延迟退休年龄有助于改善养老保险基金财务状况,降低基金收不抵支风险。具体到中国实际情况,延迟退休年龄对降低养老金隐性债务规模和缓解养老金支付压力具有积极的作用,是中国基本养老保险制度参量式改革的重要着力点(林宝,2003;张熠,2011;曾益等,2013)。关于生育政策调整对养老保险基金的影响,张思锋等(2010)指出放宽生育政策可缩减养老金缺口。孙博等(2011)的研究发现,逐步放开二孩政策下的基金缺口峰值比计划生育政策减少11.95万亿元,比"双独二孩"政策减少3.73万亿元。曾益等(2015)指出"单独二孩"政策推迟了城镇职工基本养老保险统筹基金出现累计赤字的时点。可见,延迟退休年龄和调整生育政策能增强城镇职工基本养老保险基金的偿付能力。
关于是否应该通过提高社会统筹缴费率来维持养老保险基金财务平衡,Galasso(2008)认为,要想降低人口老龄化对养老保险体系造成的负面影响,在延迟退休年龄的同时还必须提高缴费率。而国内多数学者并不赞成通过提高社会统筹缴费率来缓解中国养老金收支压力。这是因为目前企业已经承受着较重的社会保险缴费负担,提高社会统筹缴费率将进一步挤压企业盈利空间,诱发企业更大程度地逃欠养老保险缴费(孙祁祥,2001;胡秋明和景鹏,2014)。还有学者认为应适当降低社会统筹缴费率。封进(2013)指出,适当降低社会统筹缴费率可以给予企业更多的参与激励,反而会增加城镇职工基本养老保险基金收入。那么,城镇职工基本养老保险社会统筹缴费率到底是应该提高、降低,还是保持不变呢?
合理确定最优社会统筹缴费率并将其与现行政策缴费率相比较,才能判断缴费率的调整方向。国内外相关研究也表明我国城镇职工基本养老保险社会统筹缴费率存在一定的下降空间,这与十八届三中全会《决定》和"十三五"规划建议中提出的"适当降低社会保险费率"相契合。①十八届五中全会根据中国人口特征已发生历史性转变的基本国情,继"单独二孩"政策之后又一次对生育政策进行了调整,提出"全面实施一对夫妇可生育两个孩子政策"。与此同时,"十三五"规划建议明确提出"出台渐进式延迟退休年龄政策"。目前,针对生育政策调整与基本养老保险制度关系的研究并不多见,更是缺乏在全面二孩和延迟退休年龄等多种政策背景下,建立一般均衡模型测算基本养老保险最优社会统筹缴费率并考察缴费率调整对经济系统各变量的影响的研究。基于此,本文以城镇职工基本养老保险制度为例,在OLG模型一般均衡框架内,从社会福利最大化视角,测算五种生育情景下不同退休年龄的最优社会统筹缴费率,并分析降低社会统筹缴费率的经济效应。
①2015年我国失业、工伤和生育保险费率共计下降2%,今后社会保险费率下调的重点将是基本养老保险和医疗保险。
二、一般均衡模型构建(一)竞争经济模型。本文构建的竞争经济模型以两期OLG模型为基础,借鉴d’Autume(2003)和Fanti等(2013)的模型设定形式,并结合我国城镇职工基本养老保险制度的实际情况进行具体设定。假定在一个封闭且无限存续的竞争经济中存在众多异质性个人、同质性企业和一个政府,个人的决策目标是实现一生效用最大化,企业的决策目标是追求利润最大化,政府的决策目标是维持基本养老保险基金收支平衡。
1.个人决策。假设个人只生存两个时期(成年期和老年期),每期长度为1,对应的时间跨度是35年,老年期平均生存时间为T(T<1),如图1所示。每期同时存在两代人,t期所有人、成年人和老年人的数量分别为Nt、N1,t和N2,t,且Nt=(1+b)Nt-1,b为人口增长率。t期出生的个人无弹性供给1单位劳动获得工资收入wt。由于人力资本禀赋存在差异,可按人力资本含量高低将所有个人分为两类,则第i类人的工资收入为wti(i=1,2)。为考察延迟退休年龄对个人及养老保险制度的影响,我们将老年期分为两段——继续工作阶段和退休阶段,②即t期出生的个人在t+1期仍要工作一段时间Z(0≤Z<T),并获得工资收入Zwt+1,然后才能退休享受闲暇。如此,t期出生的第i类人的一生效用由一生消费和闲暇构成,用可分离的对数效用函数表示为:
\[U_t^i = ln(c_{1,t}^i) + \beta T\{ ln(c_{(2,t + 1)}^i/T) + \varphi ln[(T - Z)/T]\} \]
(1)
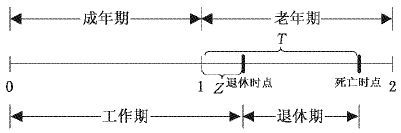
|
| 图1 个人一生阶段划分 |
②经典OLG模型假定成年期和老年期时间跨度相同(假设都为35年,20岁参加工作),个人在成年期既工作又消费,在老年期只消费不工作,那么个人退休时点是确定的(55岁退休)。如果退休年龄发生变化(60岁退休),根据经典OLG模型的假定,就必须调整成年期和老年期的时间跨度(都变为40年),相应的模型经济参数也都发生变化,致使退休年龄调整前后得出的结果不可比较。针对这一不足,本文对经典OLG模型的假设条件和模型形式进行了修正,以揭示延迟退休年龄的经济效应。
在"统账结合"的城镇职工基本养老保险制度下,t期出生的第i类人在成年期共缴纳(θ+τ)wti养老保险费,θ和τ分别为统筹账户和个人账户缴费率。成年期个人获得的工资收入除消费和缴纳养老保险费外,剩余部分都进行储蓄Sti。考虑到个人在老年期仍工作一段时间,为简化计算,本文假定在此阶段个人只缴纳统筹账户养老保险费θZwt+1i,个人账户无须缴纳。当然,如此简化会对最优社会统筹缴费率的估计结果产生一定的影响,但我们认为这种影响较小。①这样,t期出生的第i类人在t+1期的总收入包括:净工资收入(1-θ)Zwt+1i、私人储蓄本息(1+rt+1)Sti、个人账户养老金累积(1+rt+1)τwti和统筹账户养老金(T-Z)Pt+1,其中rt+1为资本回报率。根据上述假设,t期出生的第i类人在两期的消费预算约束为:
\[c_{1,t}^i = (1 - \theta - \tau )w_t^i - S_t^i\]
(2)
\[c_{2,t + 1}^i = (1 - \theta )Zw_{t + 1}^i + (1 + {r_{t + 1}})(S_t^i + \tau w_t^i) + (T - Z){P_{t + 1}}\]
(3)
①t期出生的个人在t+1期不进行个人账户缴费会降低退休后的养老金待遇,为了保持退休后消费水平不减,一方面要求提高社会统筹缴费率,另一方面个人也会增加在t期的储蓄,带动资本存量提高,从而促进工资水平上升,那么原来的社会统筹缴费率就可能会满足个人退休后的消费需要。两方面因素同时作用会较大程度地抵消对最优社会统筹缴费率的影响,而且在t+1期个人继续工作的时间也较短,因此我们认为这种简化设计对最优社会统筹缴费率的影响会很小。
平衡两期消费的欧拉方程为:
\[c_{2,t + 1}^i/c_{1,t}^i = \beta T(1 + {r_{t + 1}})\]
(4)
2.企业决策。假设企业利用物质资本Kt和劳动Lt两种要素生产最终产品。因存在人力资本禀赋差异,令第i类人提供的有效劳动为λiLti,λi为劳动生产率,则产出用C-D型生产函数表示为Yt=f(Kt,AtLt)=Ktα(λ1Lt1+λ2Lt2)1-α,α为物质资本产出弹性。Lt有两层含义:一是成年期和老年期的劳动供给,Lt=N1,t+ZN2,t=(1+b+Z)N2,t;二是高低两类人力资本型个人的劳动供给,Lt=Lt1+Lt2=(u1+u2)Lt,ui为第i类劳动者的比重。则生产函数的集约形式为yt=f(kt)=ktα,其中:yt=Yt/(λ1Lt1+λ2Lt2),kt=Kt/(λ1Lt1+λ2Lt2),分别为有效劳均产出和资本。企业利润是总产出减去劳动者工资、资本折旧和资本利息,其函数表示为:
\[{\pi _t} = {Y_t} - \sum\limits_{i = 1}^2 {w_t^iL_t^i} - ({r_t} + \delta ){K_t}\]
(5)
企业利润最大化时的资本和劳动边际报酬为:
\[{r_t} = \alpha k_t^{\alpha - 1} - \delta \]
(6)
\[w_t^i = {\lambda _i}(1 - \alpha )k_t^\alpha \]
(7)
根据两类劳动者的工资水平及其比重,可求得社会平均工资$\overline {{w_t}} $
\[\overline {{w_t}} = \sum\limits_{i = 1}^2 {{u_i}} {\lambda _i}(1 - \alpha )k_t^\alpha \]
(8)
3.政府决策。政府的职责是建立、维护或改革养老保险制度,承担制度转轨成本,兑现曾经做出的养老保险承诺,维持养老保险基金收支平衡(郑伟和孙祁祥,2003)。城镇职工基本养老保险制度的设计初衷是统筹账户与个人账户分账管理,但由于庞大的制度转轨成本无法通过统筹账户缴费来化解,又缺乏其他相对有效的筹资渠道,为了保障当期养老金足额发放,个人账户资金会被挤占。截至2014年底,城镇职工基本养老保险个人账户"空账"规模已超过3.5万亿元。数据来自于中国社科院世界社保研究中心发布的《中国养老金发展报告2015》。考虑到我国个人账户做实的难度日益增大,本文将统筹账户与个人账户合并分析,此时政府的主要职责是维持养老保险基金收支平衡,即政府向工作人口征收养老保险费用于支付退休人口的养老金。养老金预算平衡公式为:
\[\begin{array}{*{20}{l}}
{\mathop {\mathop \sum \limits^2 }\limits_{i = 1} {\mkern 1mu} \theta w_{t + 1}^i\left( {N_{1,t + 1}^i + ZN_{2,t + 1}^i} \right) + \mathop {\mathop \sum \limits^2 }\limits_{i = 1} {\mkern 1mu} \tau w_{t + 1}^iN_{1,t + 1}^i}\\
{ = \left( {T - Z} \right){P_{t + 1}}{N_{2,t + 1}} + \mathop {\mathop \sum \limits^2 }\limits_{i = 1} {\mkern 1mu} \left( {1 + {r_{t + 1}}} \right)\tau w_t^iN_{2,t + 1}^i}
\end{array}\]
(9)
4.市场出清。由于本文假定了个人在老年期继续工作阶段不再缴纳个人账户养老保险费,故每期的资本积累来自上一期的私人储蓄和个人账户养老金。资本市场出清条件为:
$${K_{(t + 1)}} = \sum\limits_{i = 1}^2 {(S_t^i + \tau w_t^i)N_{1,t}^i} $$
(10)
企业生产的最终产品和剩余资本除用于当期所有个人消费外,还需满足下期资本积累要求,则产品市场出清条件为:
$$F({K_t},{L_t}) + (1 - \delta ){K_t} = \sum\limits_{i = 1}^2 {N_{1,t}^ic_{1,t}^i + T} \sum\limits_{i = 1}^2 {N_{2,t}^ic_{2,t}^i + {K_{(t + 1)}}} $$
(11)
5.模型求解。根据上述假设,给定k1、θ和其他参数,竞争经济一般均衡要求在个人资源{c1,t,c2,t+1,St,Pt+1}、企业资源{Lt,Kt}和生产要素价格{rt,wt}下,使得:(1)个人一生效用最大化下平衡两期消费满足式(4);(2)企业利润最大化下生产要素边际报酬满足式(6)和式(7);(3)政府维持养老金预算平衡满足式(9);(4)资本市场和产品市场出清分别满足式(10)和式(11)。用差分方程描述的动态均衡条件表示如下:
$$\matrix{
{{{\left[{\beta T\left( {1 - \theta } \right) + \tau } \right]\left( {1 - \alpha } \right)k_t^\alpha } \over {1 + \beta T}} - {{Z\left( {1 - \theta } \right)\left( {1 - \alpha } \right)k_{t + 1}^\alpha } \over {\left( {1 + \beta T} \right)\left( {1 - \delta + \alpha k_{t + 1}^{\alpha - 1}} \right)}}} \hfill \cr
{ - {{\left[{\theta \left( {1 + b + Z} \right) + \left( {1 + b} \right)\tau } \right]\left( {1 - \alpha } \right)k_{t + 1}^\alpha } \over {\left( {1 + \beta T} \right)\left( {1 - \delta + \alpha k_{t + 1}^{\alpha - 1}} \right)}} = \left( {1 + {\rm{b}} + {\rm{Z}}} \right){k_{t + 1}}/\mathop {\mathop {\mathop \sum \limits^{} }\limits_{i = 1} {\mkern 1mu} }\limits^2 {\mkern 1mu} {u_i}{\lambda _i}} \hfill \cr
} $$
(12)
可以证明,当0<dkt+1/dkt<1时,竞争经济存在唯一、稳定且非振荡的稳态均衡。②稳态均衡时,kt+1=kt=k,则式(12)转变为:
$${{\left[{\beta T\left( {1 - \theta } \right) + \tau } \right]\left( {1 - \alpha } \right){k^{\alpha - 1}}} \over {1 + \beta T}} - {{\left[{Z + \left( {\theta + \tau } \right)\left( {1 + b} \right)} \right]\left( {1 - \alpha } \right){k^{\alpha - 1}}} \over {\left( {1 + \beta T} \right)\left( {1 - \delta + \alpha {k^{\alpha - 1}}} \right)}} = {{\left( {1 + {\rm{b}} + {\rm{Z}}} \right)} \over {\mathop {\mathop {\mathop \sum \limits^{} }\limits_{i = 1} {\mkern 1mu} }\limits^2 {\mkern 1mu} {u_i}{\lambda _i}}}$$
(13)
②限于篇幅控制,文中略去证明过程,读者可向作者索取。
对相关参数赋值,通过式(13)即可求出稳态有效劳均资本k*,带入上述各式就能求出竞争经济稳态时的有效劳均产出y*、生产要素价格{r*,w1*,w2*}、统筹账户养老金P*和个人福利{S1*,c11*,c21*,U1*;S2*,c12*,c22*,U2*}。
(二)社会福利模型。竞争经济模型中的稳态有效劳均资本k*是在给定社会统筹缴费率的前提下得到的,而本文更为关注的是如何确定稳态最优社会统筹缴费率。我们认为,最优社会统筹缴费率是养老保险制度内外均衡的具体表现,以实现社会福利最大化为最终目标。
观察式(13)可知,在给定相关参数值的情况下,如果得到了稳态有效劳均资本,便能求出稳态最优社会统筹缴费率。借鉴杨再贵(2008)等学者的研究思路,本文引入社会福利函数,求出社会福利最大化时的劳均资本水平,并令其等于竞争经济中的稳态有效劳均资本,从而得到最优社会统筹缴费率。本文将社会福利定义为从今以后各代人的效用贴现和,根据个人效用函数形式,社会福利函数可表示为:
$${\rm{V}} = \mathop {\mathop {\mathop \sum \limits^{} }\limits_{i = 1} {\mkern 1mu} }\limits^2 {\mkern 1mu} \left\{ {\beta T\left[{\ln \left( {{{c_{2,1}^i} \over T}} \right) + \varphi ln\left( {{{T - Z} \over T}} \right)} \right] + \mathop {\mathop {\mathop \sum \limits^{} }\limits_{t = 1} {\mkern 1mu} }\limits^\infty {\mkern 1mu} {\rho ^{t - 1}}\left\{ {\ln \left( {c_{1,t}^i} \right) + \beta T\left[{\ln \left( {{{c_{2,t + 1}^i} \over T}} \right) + \varphi ln\left( {{{T - Z} \over T}} \right)} \right]} \right\}} \right\}$$
(14)
$$f'(\bar k) = \left( {1 + b} \right)/\rho + \delta - 1$$
(15)
根据生产函数集约形式,社会福利最大化下的劳均资本水平$\bar k$:
$${\rm{k = }}{\left\{ {\left[{1 + b + \rho \left( {\delta - 1} \right)} \right]/\alpha \rho } \right\}^{{1 \over {\alpha - 1}}}}$$
(16)
令竞争经济中的稳态有效劳均资本等于社会福利最大化下的劳均资本水平,即$\tilde k = {k^*}$,带入式(13)即可得到社会福利最大化时的稳态最优社会统筹缴费率θ*:
$$\theta *{\rm{ = }}{{\beta T + \tau } \over {\beta T + \rho }}{{Z\rho + \left( {1 + b} \right)\tau \rho } \over {\left( {1 + b} \right)\left( {\beta T + \rho } \right)}}{{\alpha \rho \left( {1 + \beta T} \right)\left( {1 + b + Z} \right)} \over {\left( {1 - \alpha } \right)\left( {1 + b + \rho \delta - \rho } \right)\left( {\beta T + \rho } \right)}} \times {1 \over {\mathop {\mathop {\mathop \sum \limits^{} }\limits_{i = 1} {\mkern 1mu} }\limits^2 {\mkern 1mu} {u_i}{\lambda _i}}}$$
(17)
由此可见,最优社会统筹缴费率θ*由人口增长率b、退休年龄Z、预期寿命T、个人账户缴费率τ、物质资本产出弹性α、个人主观效用贴现因子β、社会贴现因子ρ、资本折旧率δ、劳动者类型ui和劳动生产率λi等参数共同决定。显然,唯有合理设定这些参数值才能得到稳健可靠的最优社会统筹缴费率。此外,通过该式还可以分析生育政策调整和退休年龄延迟对最优社会统筹缴费率的影响。
三、参数取值及说明(一)经济参数。
1.物质资本产出弹性α。已有研究对中国物质资本产出弹性的取值差别较大,林忠晶和龚六堂(2008)指出,如果生产函数是C-D型时,中国物质资本产出弹性的取值范围在0.3-0.8之间,他们取值为0.65;邵宜航等(2010)、彭浩然和陈斌开(2012)都设为0.5;杨再贵(2008)、康传坤和楚天舒(2014)都设为0.35。由于社会统筹缴费率不能为负,根据上述模型并结合其他参数取值可以算出α的上限约为0.533。考虑到中国人口红利的逐渐消失以及劳动力人力资本禀赋的不断提升,可以判断未来中国物质资本产出弹性将有所下降。此外,实际经济中的物质资本产出弹性受市场竞争、财政支出和产业结构等多种因素的影响,本文并未将这些因素纳入模型,所以这里的α应小于真实物质资本产出弹性。经过权衡取舍,本文将α的基准值设定为0.4,并对其进行敏感性分析。
2.资本折旧率δ。众多文献通常将年度资本折旧率设为0.1,本文也如此设定,即设δ的基准值为0.9722。
3.劳动生产率λi。人力资本禀赋高低决定着劳动生产率大小,反映在工资水平上,由式(7)可得wt1/wt2=λ1/λ2。参考邹铁钉和叶航(2014)的做法,将高、低两类人力资本型劳动者的工资水平分别用国有单位和城镇集体单位的平均工资代替。统计资料显示,历年来国有单位与城镇集体单位的平均工资比基本保持在1.5左右,即λ1/λ2=1.5。假定未来两类劳动者的劳动生产率保持不变,令低人力资本劳动生产率λ2=1,则λ1=1.5。
(二)人口参数。
1.人口增长率b。本文采用队列要素法预测中国未来人口总数,具体过程为:以"六普"数据为基础,将人口按年龄和性别分成不同队列,通过估计总和生育率、生育模式和出生性别比来预测每年人口出生情况,通过估计预期寿命和死亡模式来预测每年人口死亡情况,最终得到每年分年龄和性别的人口数。相对而言,合理确定总和生育率对准确预测人口总数尤为重要。"六普"数据显示,2010年中国总和生育率为1.18,但由于存在瞒报和漏报等情况,导致该值低于真实水平。学者们采用多种方法对总和生育率进行校正和重新估计,认为2010年中国总和生育率在1.4-1.6之间(崔红艳等,2013;王金营和戈艳霞,2013)。陈卫和杨胜慧(2014)也指出我国总和生育率不会低于1.5。由此,本文将2010年总和生育率取值为1.5。对其他人口预测参数的设定,生育模式用年龄别规格化生育率表示,假设未来生育模式与"六普"公布的相同;出生性别比假设由2010年的118下降到2015年的115,之后每年降低0.3,2045年及以后保持106不变;基于联合国最新发布的《世界人口展望2015版》预测人口预期寿命,并结合我国实际情况进行适当调整;死亡模式采用远东生命表来估计未来每年分年龄和性别的死亡率。
要想合理估计全面二孩政策实施后中国未来总和生育率水平,就必须要确定出符合政策规定育龄妇女的数量和生育意愿。翟振武等(2014)利用2005年全国1%人口抽样调查数据推算得到,2012年我国全面放开二孩政策后的目标人群规模为1.52亿人。2010年我国妇女规模为3.79亿人,简单换算后约有40%的妇女符合全面二孩政策规定。由于妇女生育意愿会受到家庭经济压力及职业发展规划等因素的影响,因此本文假设了五种生育情景,即0%、20%、50%、80%和100%符合规定的育龄妇女将生育二孩,据此估计从2016年起实施全面二孩政策后总和生育率的变化情况。
根据以上人口参数假设,采用PADIS-INT软件预测全面二孩政策实施后五种生育情景下的中国未来人口总数。由于模型每期时间跨度是35年,我们选取2016-2050年这一时期考察生育政策调整对人口增长率和社会统筹缴费率的影响。本文选择"城镇人口"这一统计口径,用总人口×城镇化率来衡量。假设城镇化率由2016年的55%上升到2050年的75%,根据人口预测结果,计算得到五种生育情景下2016-2050年中国城镇人口增长率b分别为0.2969、0.3104、0.3310、0.3518和0.3658。
2.人口预期寿命T。根据联合国最新发布的《世界人口展望2015版》中对中国人口预期寿命的预测,结合我国实际情况进行适当调整,本文假设2050年中国人口预期寿命为83.01岁,由此T的基准值为0.8003。
3.两类劳动者比重ui。本文用大专及以上学历就业人员比重表征高人力资本型劳动者比重,用大专以下学历就业人员比重表征低人力资本型劳动者比重。据《中国统计年鉴》数据显示,近年来我国大专及以上学历就业人口比重逐年递增,考虑到居民对教育的日益重视以及高等教育大众化、普及化的发展,可以预测未来高人力资本型劳动者比重将大幅提高。基于此,本文假设u1=0.25,u2=0.75,并对其进行敏感性分析。
(三)贴现参数。
1.个人主观效用贴现因子β。个人主观效用贴现因子的计算公式为β=1/T(1+γ),γ为时间贴现率。邵宜航等(2010)、康传坤和楚天舒(2014)将年度时间贴现率取值为0.01,本文也如此设定,故γ=0.4026,从而β=0.8909,对其进行敏感性分析。
2.社会贴现因子ρ。社会贴现因子反映了政府对各代人效用和利益的重视程度,社会贴现因子越大,意味着政府对未来代的责任感越强。Song等(2015)在研究养老金代际共享问题时将社会贴现率假设为真实市场利率,蒋云赟(2009)指出,社会贴现率与经济增长率之间存在一定的关联。基于此,本文将社会贴现率定义为实际经济增长率,假设2016-2050年中国平均名义经济增长率为5.5%,平均通货膨胀率为3%,由此计算得到ρ=0.4319,并对其进行敏感性分析。
3.个人对闲暇的偏好率φ。从上述模型推导公式可知,个人对闲暇的偏好率只对个人效用和社会福利产生影响,不会对社会统筹缴费率产生影响,故取φ=1.5。
(四)制度参数。
1.退休年龄Z。本文在构建模型时假设个人出生后便参加工作,但现实并非如此,需要考虑个人实际参加工作年龄,真正意义上的OLG模型初始时点是从个人参加工作开始的。遵循众多文献的做法,本文以20岁作为个人参加工作的起始年龄,那么成年期末个人年龄就是55岁。全国"十三五"规划建议提出"出台渐进式延迟退休年龄政策",尽管目前国家尚未公布具体的延迟退休方案,但可以肯定到2050年退休年龄至少延长5-10岁。假定当前城镇职工平均退休年龄为55岁,人力资源和社会保障部部长尹蔚民在介绍"十二五"以来就业和社会保障事业发展取得的成就时指出,目前我国平均退休年龄不到55岁。考虑到该数据统计口径包括体制外劳动者(农民工和个体商户等),拉低了城镇职工平均退休年龄,由此本文将目前城镇职工平均退休年龄设定为55岁。文中所指的退休年龄均为城镇职工平均退休年龄。那么2050年退休年龄就为60或65岁,则Z=1/7或2/7。
2.个人账户缴费率τ。《国务院关于完善企业职工基本养老保险制度的决定》规定,个人账户缴费率自2006年起为本人缴费工资的8%,且全部由个人缴费构成,故τ=0.08。参数基准值整理于表1中。
(一)最优社会统筹缴费率。在上文模型推导和参数取值的基础上,本文测算了五种生育情景下不同退休年龄的最优社会统筹缴费率,结果如表2所示。生育情景1是符合全面二孩政策规定的妇女都不生育二孩的极端情况,该生育情景下的人口增长率为0.2969。当退休年龄为55岁时,社会福利最大且经济系统处于一般均衡状态时的最优社会统筹缴费率为27.59%,高于目前20%的统筹账户政策缴费率。这意味着如果我国不延迟退休年龄,为维持城镇职工基本养老保险统筹账户收支平衡,就必须提高社会统筹缴费率,这显然会进一步加重企业负担。结果同时显示,随着退休年龄的不断延长,最优社会统筹缴费率将逐渐下降。退休年龄为60岁和65岁时的最优社会统筹缴费率分别为19.18%和10.77%,这表明延迟退休年龄有助于降低社会统筹缴费率。
| 情景 | 参数条件下的b值 | 退休年龄 | ||
| 55岁 | 60岁 | 65岁 | ||
| 生育情景1 | b=0.2969 | 27.59% | 19.18% | 10.77% |
| 生育情景2 | b=0.3104 | 27.60% | 19.27% | 10.95% |
| 生育情景3 | b=0.3310 | 27.60% | 19.41% | 11.21% |
| 生育情景4 | b=0.3518 | 27.61% | 19.54% | 11.47% |
| 生育情景5 | b=0.3658 | 27.61% | 19.63% | 11.64% |
| 注:参数取值为:α=0.4, δ=0.9722, β=0.8909, ρ=0.4319,T=0.8003,u1λ1+u2λ2=1.125。 | ||||
生育情景2-5是符合全面二孩政策规定的部分或全部妇女生育二孩的情况,通过与生育情景1进行对比分析,可以反映出生育政策调整对最优社会统筹缴费率的影响。符合全面二孩政策规定的育龄妇女生育二孩的比重由0%增加到100%,会使60岁退休时的最优社会统筹缴费率降到19.18%-19.63%,使65岁退休时的最优缴费率降到10.77%-11.64%。这说明随着符合规定妇女生育二孩比重的不断增加,最优社会统筹缴费率呈缓慢上升的变化趋势,即人口增长率与最优社会统筹缴费率呈正向变动关系。不同生育情景下的最优社会统筹缴费率差别不大,其原因是由于全面二孩政策存在时滞效应,新生人口不可能立即参保缴费,需要等到2036年第一批"新生二孩"加入基本养老保险制度后才会逐渐发挥作用。加之本文考察的时期是2016-2050年,从而导致生育政策调整对最优社会统筹缴费率的影响程度更加弱化。此外,退休年龄为55岁时不同生育情景下的最优社会统筹缴费率几乎相同,这是因为此时Z=0,代入式(17)后可以看出,人口增长率变化对最优社会统筹缴费率的影响很小。五种生育情景下,退休年龄为60岁时的最优社会统筹缴费率都略低于20%;当退休年龄延长到65岁时,最优缴费率则接近政策缴费率的一半,这时我国城镇职工基本养老保险社会统筹缴费率将从世界较高水平降到世界平均水平。笔者根据世界银行公布的2014年各国养老保险缴费率数据资料统计得出,在剔除数据缺失后的134个国家和地区中,养老保险体系第一支柱的雇主(企业)平均缴费率为10.2%,我国的缴费率水平与俄罗斯并列第13位。因此,为减轻企业负担、提高企业参保缴费积极性和增强制度筹资稳定性,在延迟退休年龄的同时应适当降低社会统筹缴费率。
总体而言,最优社会统筹缴费率随退休年龄的延长而下降,随人口增长率的上升而提高。当其他参数不变时,随着退休年龄的延长,养老保险缴费人数将增加且待遇领取人数将减少,养老保险基金净收入增加,在确定的养老金待遇下便可以降低社会统筹缴费率。然而,人口增长率上升在养老金预算平衡公式中表现为社会统筹缴费率下降,但测算结果却显示为提高,这似乎与现有的研究结论相违背。曾益等(2015)建立精算模型发现,在维持统筹账户原有财务状况的前提下,10%-100%符合"单独二孩"政策规定的夫妇生育二孩将使社会统筹缴费率下降至16.55%-19.57%。于洪和曾益(2015)也指出"单独二孩"政策为降低基本养老保险缴费率提供了空间。上述研究皆表明生育政策调整所带来的人口增长率上升将有助于降低社会统筹缴费率,但这一结论主要是着眼于养老保险制度本身,通过精算模型分析而来,但如果从整个经济系统的一般均衡角度进行考察,本文得出的结论在经济学逻辑上是合理的。对此,我们从两个方面进行了解释:一方面,人口增长率上升使有效劳均资本降低,人口增长率上升会提高少儿抚养比,但提高幅度受生育意愿影响;与此同时,不可逆转的人口老龄化将使得老年抚养比快速提高。由于少儿和老年抚养比与储蓄率呈负相关关系(王德文等,2004;董丽霞和赵文哲,2011),因此少儿和老年抚养比的共同提高会降低储蓄,从而导致物质资本存量减少。从而带来工资收入和私人储蓄减少,工资收入减少又会导致统筹账户养老金下降,个人退休后的财富减少。为了保障个人退休后消费水平不降,政府就会提高社会统筹缴费率。另一方面,人口增长率上升将直接导致养老保险缴费人数增加,相对较低的社会统筹缴费率即可维持统筹账户收支平衡,但这一条件能否实现受到全面二孩政策实施效果和时滞效应的影响。测算结果显示,在经济系统达到一般均衡的状态下,人口增长率上升引起最优社会统筹缴费率上升幅度超过其下降幅度,从而导致最优社会统筹缴费率提高。
(二)敏感性分析。尽管本文重点关注生育政策调整和退休年龄延迟对最优社会统筹缴费率的影响,但在社会福利最大化下,经济系统达到一般均衡状态时的最优社会统筹缴费率的确定还有赖于其他参数取值的合理性。为检验上文测算结果的稳健性,本部分将对决定最优社会统筹缴费率的几个关键参数(物质资本产出弹性α、个人主观效用贴现因子β、社会贴现因子ρ和两类劳动者比重ui)进行敏感性分析,考察这些参数变动对最优社会统筹缴费率的影响。由于不同退休年龄下各参数变动对最优社会统筹缴费率的分析思路相同,仅仅是影响程度有所差异,为此我们只对退休年龄为65岁时的五种生育情景展开分析,结果如表3所示。
| 参数取值 | 生育情景1 | 生育情景2 | 生育情景3 | 生育情景4 | 生育情景5 | 平均弹性 | |
| 基准值 | 10.77% | 10.95% | 11.21% | 11.47% | 11.64% | ||
| α | 0.44 | 2.35% | 2.54% | 2.83% | 3.11% | 3.30% | -7.49 |
| 0.36 | 18.14% | 18.30% | 18.54% | 18.78% | 18.94% | 6.55 | |
| β | 0.9799 | 14.15% | 14.32% | 14.57% | 14.82% | 14.98% | 3.00 |
| 0.8018 | 6.94% | 7.12% | 7.40% | 7.67% | 7.84% | -3.41 | |
| ρ | 0.4751 | 4.69% | 4.88% | 5.16% | 5.44% | 5.62% | -5.40 |
| 0.3887 | 17.31% | 17.48% | 17.72% | 17.97% | 18.12% | 5.82 | |
| u1 | 0.275 | 11.29% | 11.46% | 11.73% | 11.98% | 12.15% | 0.46 |
| 0.225 | 10.24% | 10.42% | 10.68% | 10.94% | 11.11% | -0.47 | |
| 注:由于u1+u2=1,确定了u1就能得到u2,故u2的敏感性分析没有在表2中列示;α、β、ρ、u1的取值是在其基准值上下变动10%。 | |||||||
从表3可以看出,五种生育情景下,物质资本产出弹性α与最优社会统筹缴费率θ*呈反向变动关系,α在基准值上下变动1%将导致θ*平均减增7.49%和6.55%。α越大,个人在老年期的资本回报就越多,工作期不用缴纳过多的养老保险费就能保证老年期消费水平不降,于是社会统筹缴费率下降的空间就越大。个人主观效用贴现因子β与最优社会统筹缴费率θ*呈正向变动关系,β在基准值上下变动1%将导致θ*平均增减3.00%和3.41%。β越大,个人越看重老年期消费,那么就需要积累足够的财富来满足其老年消费,因而政府就必须通过提高社会统筹缴费率来提升统筹账户养老金待遇水平。社会贴现因子ρ与最优社会统筹缴费率θ*呈反向变动关系,ρ在基准值上下变动1%将导致θ*平均减增5.40%和5.82%。ρ越大,意味着政府对未来各代人的责任感增强,说明政府更看重长远利益,于是会降低社会统筹缴费率来满足个人消费需求。高人力资本型劳动者比重u1与最优社会统筹缴费率θ*呈正向变动关系,u1在基准值上下变动1%将导致θ*平均增减0.46%和0.47%。u1越大,有效劳均资本越低,使得工资收入和私人储蓄减少,进而导致统筹账户养老金下降,政府就必须提高社会统筹缴费率以保障个人退休后消费水平不降。
从敏感性分析可知,最优社会统筹缴费率的确受这些参数的影响,θ*对α、β、ρ变动的敏感性相对较强,对u1变动的敏感性则相对较弱。因此,我们在做出是否降低社会统筹缴费率的决策前,需要充分考虑这些参数取值的合理性,尤其要重点关注未来物质资本产出弹性、个人主观效用贴现因子和社会贴现因子的变化。
(三)降低社会统筹缴费率的经济效应。可持续的城镇职工基本养老保险制度不仅要着眼于维持基金长期财务平衡,还要能以一定的传导机制促进经济增长和增进社会福利(胡秋明,2011)。上文测算结果已表明,五种生育情景下退休年龄为60岁或65时的最优社会统筹缴费率均低于20%,说明延迟退休年龄为降低社会统筹缴费率的改革提供了基础。基于此,如果政府在实施延迟退休政策后决定降低社会统筹缴费率,那么这一举措会产生怎样的经济效应呢?本文就从资本与产出、生产要素价格、个人福利和统筹账户养老金四个角度考察降低社会统筹缴费率的经济效应。由于不同生育情景和退休年龄下的分析思路相同,这里我们主要在生育情景2和退休年龄为65岁的情形下,模拟分析社会统筹缴费率从政策规定的20%逐步降低到最优的10.95%时经济系统各变量的变化情况,结果如表4所示。
| 经济变量 | 符号 | 20% | 18% | 16% | 14% | 12% | 10.95% | |
| 资本与产出 | k* | 0.0271 | 5.68% | 11.66% | 17.90% | 24.44% | 27.98% | |
| y* | 0.2361 | 2.24% | 4.53% | 6.82% | 9.15% | 10.38% | ||
| 生产要素价格 | r* | 2.5140 | -4.53% | -8.87% | -13.05% | -17.06% | -19.09% | |
| w1* | 0.2125 | 2.26% | 4.52% | 6.82% | 9.13% | 10.40% | ||
| w2* | 0.1417 | 2.19% | 4.52% | 6.77% | 9.10% | 10.37% | ||
| wt* | 0.1594 | 2.20% | 4.52% | 6.78% | 9.10% | 10.35% | ||
| 个人福利 | 高人力资本型 | S1* | 0.0313 | 8.54% | 17.50% | 26.90% | 36.76% | 42.13% |
| c11* | 0.1217 | 4.19% | 8.55% | 12.90% | 17.34% | 19.72% | ||
| c21* | 0.3050 | 0.82% | 1.61% | 2.33% | 2.98% | 3.34% | ||
| U1* | -3.2660 | -1.44% | -2.85% | -4.19% | -5.54% | -6.22% | ||
| 低人力资本型 | S2* | 0.0160 | 11.79% | 24.27% | 37.55% | 51.59% | 59.26% | |
| c12* | 0.0860 | 3.83% | 7.71% | 11.64% | 15.62% | 17.72% | ||
| c22* | 0.2154 | 0.46% | 0.88% | 1.21% | 1.53% | 1.67% | ||
| U2* | -3.8620 | -1.06% | -2.10% | -3.08% | -4.04% | -4.53% | ||
| 统筹账户养老金 | PT-Z* | 0.1689 | -5.51% | -11.19% | -17.11% | -23.33% | -26.64% | |
| 注:PT-Z*=(T-Z)P*,表示个人退休后获得的统筹账户养老金收入。表4中只有社会统筹缴费率为20%的那一列用绝对数表示,其他各列均用相对数表示,反映了相对于20%缴费率时各经济变量的变化程度。 | ||||||||
观察表4发现,降低社会统筹缴费率将导致资本回报率和统筹账户养老金减少,而其他经济变量值都有不同程度的增加。具体而言,从资本与产出以及生产要素价格角度看,降低社会统筹缴费率提高了稳态有效劳均资本,进而促进了稳态有效劳均产出、各类劳动者工资收入和社会平均工资的增长,但同时也会造成资本回报率下降。从统筹账户养老金角度看,降低社会统筹缴费率将使得统筹账户养老金减少,其原因在于:一方面,根据养老金预算平衡公式,当其他参数不变时,降低社会统筹缴费率会直接导致统筹账户养老金减少;另一方面,社会统筹缴费率降低引起的社会平均工资增加又间接提升了统筹账户养老金的待遇水平,但这种间接提升效应弱于直接降低效应,最终将会导致统筹账户养老金减少。
从个人福利角度看,降低社会统筹缴费率将使得各类消费、私人储蓄和个人一生效用都有所增加。降低社会统筹缴费率提高了个人工资收入,将在满足成年期消费需要和缴纳较少养老保险费后的剩余财富都进行储蓄,必然会增加私人储蓄。个人成年期消费增加的原因有两个:其一,降低社会统筹缴费率增加了工资收入,个人在成年期将拥有更多的可支配收入来提高其消费水平;其二,为积累充足的财富以保障退休后的消费水平不降,个人会增加私人储蓄,于是就会适当减少其成年期消费。最终,降低社会统筹缴费率对个人成年期消费带来的促进效应更大,从而提高了成年期消费水平。同样地,降低社会统筹缴费率对个人老年期消费的影响也包括两个方面:一方面,降低社会统筹缴费率使工资收入和私人储蓄增加,个人在老年期会拥有足够多的财富,进而促进其老年期消费水平的上升;另一方面,降低社会统筹缴费率会直接导致统筹账户养老金减少,使得个人老年期消费水平下降。模拟结果显示,社会统筹缴费率下降对老年期消费的促进作用略大于抑制作用,从而略微提高了老年期消费水平。高低两类人力资本型个人在两期消费水平的共同提高最终使其一生效用增加,进而实现社会福利的增进。
综上所述,在统筹账户收支平衡的前提下降低社会统筹缴费率,促进了经济增长并增进了社会福利,具有积极的经济效应。尽管降低社会统筹缴费率会导致统筹账户养老金减少,但工资收入增长引起的私人储蓄增加弥补了统筹账户养老金减少带来的消费损失,使个人老年期消费水平略微提高的同时还较大幅度地增加了年轻期消费。此外,降低社会统筹缴费率可以减轻企业负担,调动企业参保缴费积极性,形成一种自觉、自愿的缴费氛围,同时也为企业年金和商业养老保险留出发展空间。可见,降低社会统筹缴费率,不仅有助于完善我国多层次养老保险体系,而且有助于推进养老保险制度与经济系统的良性协调发展。
五、结论与启示本文从社会福利最大化视角,建立一般均衡模型,对五种生育情景下不同退休年龄的城镇职工基本养老保险最优社会统筹缴费率进行测算,并考察降低社会统筹缴费率对经济系统各变量的影响,得到如下主要结论:第一,最优社会统筹缴费率随退休年龄的延长而下降,随人口增长率的上升而提高。在合理的参数设定下,0%-100%符合全面二孩政策规定的妇女生育二孩,将使退休年龄为60岁时的最优社会统筹缴费率降到19.18%-19.63%,使退休年龄为65岁时的最优缴费率降到10.77%-11.64%。最优社会统筹缴费率随人口增长率上升而提高的结论是从经济系统一般均衡角度分析得出的,这与只着眼于养老保险制度本身而得到的结论相反。不同生育情景下最优缴费率变化不大的原因是由于全面二孩政策存在时滞效应,要到2036年才开始逐渐发挥作用。第二,除了受生育政策和退休年龄影响外,最优社会统筹缴费率对物质资本产出弹性、个人主观效用贴现因子和社会贴现因子的敏感性也较强。因此,政策制定者在做出是否降低社会统筹缴费率的决策前,需要充分考虑参数取值的合理性。第三,降低社会统筹缴费率具有积极的经济效应,不仅能促进经济增长和增进社会福利,而且有助于完善我国多层次养老保险体系,推进养老保险制度与经济系统的良性协调发展。
基于上述结论,本文得到如下启示:第一,抓紧实施延迟退休年龄政策。当前的退休制度已难以适应社会经济发展需要,而且延迟退休年龄为增强基本养老保险制度偿付能力和降低社会统筹缴费率提供了基础,结合中国的实际情况,应及早推出并实施渐进式延迟退休年龄政策。第二,适势、适时、适当降低城镇职工基本养老保险社会统筹缴费率。根据宏观经济发展形势、基本养老保险基金结余情况、财政补贴水平和企业盈利能力等因素,在恰当的时机,采取渐进平稳的方式确定适当的下降幅度。第三,借助制度外力量化解养老保险制度的转轨成本。目前社会统筹政策缴费率之所以偏高是因为企业承担了部分转轨成本,将企业额外缴费负担转嫁出去是降低政策缴费率的根本。政府可通过国有资产划拨、国企让利、财政补贴和发行国债等方式积极筹措资金来逐步化解庞大的制度转轨成本。
当然,本文的研究仍存在一些不足:首先,本文采用的两期OLG模型,难以刻画真实的人口变动特征和反映渐进式延迟退休年龄政策的效果,测算得出的最优社会统筹缴费率难免存在一定的误差;其次,本文只是确定了不同生育情景下不同退休年龄的最优社会统筹缴费率,而对降低社会统筹缴费率的具体路径安排和阶段划分没有展开详细论述。在后续研究中,可采用更多期OLG模型或DSGE模型与精算技术相结合来解决上述不足,进一步探讨全面二孩政策和延迟退休年龄对经济系统及基本养老保险制度的影响。
| [1] | 陈卫,杨胜慧.中国2010年总和生育率的再估计[J].人口研究,2014,(6):16-24. |
| [2] | 崔红艳,徐岚,李睿.对2010年人口普查数据准确性的估计[J].人口研究,2013,(1):10-21. |
| [3] | 封进.中国城镇职工社会保险制度的参与激励[J].经济研究,2013,(7):104-117. |
| [4] | 胡秋明.可持续养老金制度改革的理论与政策分析[M].北京:中国劳动社会保障出版社,2011. |
| [5] | 胡秋明,景鹏.社会保险缴费主体逃欠费行为关系演变与调适[J].财经科学,2014,(10):19-28. |
| [6] | 康传坤,楚天舒.人口老龄化与最优养老金缴费率[J].世界经济,2014,(4):139-160. |
| [7] | 于洪,曾益.退休年龄、生育政策与中国基本养老保险基金的可持续性[J].财经研究,2015,(6):46-57. |
| [8] | 曾益,任超然,刘倩.破解养老金支付危机:"单独二孩"政策有效吗?——以城镇职工基本养老保险为例[J].财经研究,2015,(1):21-34. |
| [9] | 翟振武,张现苓,靳永爱.立即全面放开二胎政策的人口学后果分析[J].人口研究,2014,(2):3-17. |
| [10] | 张熠.延迟退休年龄与养老保险收支余额:作用机制及政策效应[J].财经研究,2011,(7):4-16. |
| [11] | Fanti L,Gori L,Sodini M. Complex dynamics in an OLG model of neoclassical growth with endogenous retirement age and public pensions[J].Nonlinear Analysis:Real World Applications,2013,14(1):829-841. |
| [12] | Song Z,Storesletten K,Wang Y,Zilibotti F. Sharing high growth across generations:Pensions and demographic transition in China[J].American Economic Journal:Macroeconomics,2015,7(2):1-39. |
 2016, Vol. 42
2016, Vol. 42


