文章信息
- 刘华军, 何礼伟
- Liu Huajun, He Liwei
- 中国省际经济增长的空间关联网络结构——基于非线性Granger因果检验方法的再考察
- The Spatial Network Structure of China's Provincial Economic Growth: Re-examination Based on Nonlinear Granger Causality Test
- 财经研究, 2016, 42(2): 97-107
- Journal of Finance and Economics, 2016, 42(2): 97-107.
-
文章历史
- 收稿日期:2015-10-22
一、引 言
伴随着国家区域发展总体战略的相继实施,以及“京津冀协同发展”和“长江经济带”等新的区域发展战略的提出,区域经济的空间关联日趋加强并成为区域协调发展的重要决策变量和目标。党的十八届五中全会聚焦全面建成小康社会的目标,提出协调发展理念,着重解决发展不平衡问题,这是党中央着眼未来谋划全局的战略考量,进而可以不断开创各地区相互促进、区域协同推进的良好发展局面。不断完善区域政策,促进各地区协调发展、协同发展、共同发展已成为中国区域经济发展的“新常态”。与此同时,在区域经济协调发展战略以及市场机制双重力量的共同推动下,区域之间要素的自由流动和商品的自由贸易以及经济活动带来的知识溢出,不断加深了区域之间的经济联系,中国区域经济增长呈现出显著的空间关联性(Ying,2000和2003;陈秀山和张可云,2005;Groenewold等,2007和2008;潘文卿,2012;等),而且区域经济的空间关联关系已经突破了传统的线性模式,逐步呈现出系统的、复杂的和多线程的网络结构形态(李敬等,2014)。从网络的角度重新审视社会经济空间组织构架也成为未来研究的新趋势(李国平等,2012)。在此背景下,深入揭示中国区域经济空间关联的整体网络结构及其效应,对中国新时期打造中国区域经济的“升级版”并最终实现“以点带面、从线到片,逐步形成区域大合作”的区域经济一体化宏伟蓝图,夺取全面建成小康社会决胜阶段的伟大胜利具有重大现实意义。
从已有研究进展看,李敬等(2014)利用1978-2012年中国分省数据,以Granger因果检验技术识别省际经济增长的空间关联关系,并利用社会网络分析(Social Network Analysis,SNA)刻画了中国经济增长空间关联的网络结构特征。该文的贡献并非在于SNA的应用,而在于采用Granger因果检验技术识别省际经济增长之间的传导关系。此后刘华军等(2015a和b)基于不同的指标运用相同方法刻画了中国经济增长的空间网络结构特征。然而,上述文献采用的均是线性Granger模型,无法考虑经济增长的非线性趋势。正如Granger和Newbold(1986)所指出的,真实世界几乎都是非线性关系组成的,非线性模型代表了模拟真实世界的正确方向。鉴于已有研究的局限,本文立足于中国经济增长空间分布格局的基本国情,在VAR框架下利用Baek和Brock(1992)、Hiemstra和Jones(1994)以及Diks和Panchenko(2006)提出的非线性Granger因果检验方法(Non-linear Granger Causality Test),识别中国省际经济增长之间的非线性传导效应,并在此基础上利用SNA工具揭示其联动网络结构特征。
二、方法与数据(一)识别经济增长的空间非线性溢出效应。在VAR框架下,Granger因果检验方法将所有变量均视为内生变量,不需要过多关于变量间关系的先验约束,能够得出一组变量是否有助于改善另一组变量预测的信息。然而,传统的Granger检验方法仅可以揭示变量之间的线性“因果”关系,却因忽视实际存在的非线性关系而导致结论出现偏差。为了克服线性Granger因果检验方法的局限,Baek和Brock(1992)、Hiemstra和Jones(1994)以及Diks和Panchenko(2006)构建了基于非参数统计量的检验方法,该方法基于线性Granger因果模型过滤掉序列间的线性“预测能力”,从残差中提取相应信息来分析非线性Granger因果关系。
1.线性Granger因果检验方法。该方法由Granger(1969)提出,回答了一个时间序列的历史信息(滞后值)是否能够提高对另一个时间序列当期值的预测能力的问题,可以检验一个变量是否在时间上“领先”(precede)于另一个变量。如果一个时间序列的历史信息无助于改进另一时间序列当期值的预测能力,则称前者不是后者的Granger原因(causality);否则,则称前者是后者的Granger原因。①出于简易操作的考虑,对两个时间序列进行Granger因果检验,并在VAR模型框架下进行检验,可由式(1)、式(2)推导得出。其中,Xt、Yt是两个时间序列变量;α、β、δ和φ是被估计参数;ε1、ε2是残差序列;θ1、θ2、θ3及θ4为滞后阶数。
① 需要强调指出的是,Granger因果关系检验中的“因果”(causality)概念更多地是基于统计学而非基于传统哲学意义(陈雄兵和张宗成,2008;Wooldridge,2012)。
| ${X_t} = \sum\limits_{i = 1}^{{\theta _1}} {{\alpha _i}} {X_{t - i}} + \sum\limits_{j = 1}^{{\theta _2}} {{\beta _i}} {Y_{t - j}} + {\varepsilon _{1,t}}$ | (1) |
| ${Y_t} = \sum\limits_{i = 1}^{{\theta _3}} {{\delta _i}} {Y_{t - i}} + \sum\limits_{j = 1}^{{\theta _4}} {{\varphi _i}} {X_{t - j}} + {\varepsilon _{2,t}}$ | (2) |
2.BDS检验。在非线性Granger因果检验之前,需要对时间序列进行非线性检验,通常采用BDS方法(Broock等,1996),该方法基于跨期空间概率(spatial probabilities across time)的估计量来检验时间序列是否是独立同分布。BDS检验通过式(1)和式(2)的VAR模型剔除线性关系得到残差序列ε1、ε2,用来检验残差序列是否独立同分布,如果拒绝独立同分布的原假设,那么残差序列就存在非线性趋势。在这种情况下,非线性Granger因果检验可能更为恰当。BDS检验给定一个m维的时间序列Zt,其观测值为(zt,zt+1,…,zt+m-1)。跨期空间概率的估计量关联积分的定义是:
| ${C_m}\left( {T,d} \right) = \sum\nolimits_{t = 1}^{{T_m} - 1} {\sum\nolimits_{s = t + 1}^{{T_m} - 1} {I\left( {Z_t^m,Z_s^m,d} \right)} \times \left[{2/{T_m}\left( {{T_m} - 1} \right)} \right]} $ | (3) |
其中:I(Ztm,Zsm,d)是指标函数(Indicator Function),当I函数满足条件‖Ztm,Zsm‖<d时,I(Ztm,Zsm,d)=1;否则,I(Ztm,Zsm,d)=0。‖Ztm,Zsm‖为两个序列Ztm、Zsm间的欧式空间距离,d是带宽,T是总样本数,序列Zt可以分为Tm个m维的子样本,且Ztm=(zt,zt+1,…,zt+m-1),Zsm=(zt,zt+1,…,zt+m)。
那么,可对BDS检验的统计量做出如下定义:
| ${W_m}\left( {T,d} \right) = \sqrt {T\left[{{C_m}\left( {T,d} \right) - {C_1}{{\left( {T,d} \right)}^m}} \right]} /{\sigma _m}\left( d \right)$ | (4) |
其中:σm(d)是给定m维样本的标准差。BDS统计量Wm(T,d)渐进服从标准正态分布,如果BDS统计量拒绝原假设,则表明存在非线性关系。
3.非线性Granger因果关系检验。Diks和Panchenko(2006)基于线性Granger因果模型过滤掉序列间的线性“预测能力”,从残差中提取相应信息来分析非线性Granger因果关系。仍然考虑Xt、Yt是两个时间序列变量,定义Xt的m维领先向量(leading vector)为Xtm,Xt的Lx期滞后向量(lag vector)和Yt 的Ly期滞后向量分别为Xt-LxLx和Yt-LyLy,见公式(5):
| $\begin{array}{l} X_t^m = \left( {{x_t},{x_{t + 1}},\cdots ,{x_{t + m - 1}}} \right),m = 1,2,\cdots ;t = 1,2 \cdots \\ X_{t - Lx}^{Lx} = \left( {{x_{t - Lx}},{x_{t - Lx + 1}},\cdots ,{x_{t - 1}}} \right),Lx = 1,2,\cdots ;t = Lx + 1,Lx + 2 \cdots \\ Y_{t - Ly}^{Ly} = \left( {{y_{t - Ly}},{y_{t - Ly + 1}},\cdots ,{y_{t - 1}}} \right),Ly = 1,2,\cdots ;t = Ly + 1,Ly + 2 \cdots \end{array}$ | (5) |
给定值m、Lx、Ly>1以及任意小的常数d>0,若Y满足式(6)的条件概率,则Y不是X的严格非线性Granger原因。其中,Pr(·)表示概率,‖·‖表示最大范数(Norm)。s,t=max(Lx,Ly)+1,...,T-m+1。如果给定式(6)右边序列Xt的条件概率(即滞后序列对领先序列的影响概率),且无论有无序列Yt作为条件都不会对其产生影响,则表明Y不是影响X的Granger原因。式(6)中的条件概率也可以用式(7)来表达:
| $\begin{array}{l} \Pr \left( {\left\| {X_t^m - X_s^m} \right\| < d\left| {\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d,\left\| {X_{t - Ly}^{Ly} - X_{s - Ly}^{Ly}} \right\| < d} \right.} \right)\\ = \Pr \left( {\left\| {X_t^m - X_s^m} \right\| < d\left| {\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d} \right.} \right) \end{array}$ | (6) |
| $CI = \left( {m + Lx,Ly,d} \right)/CI\left( {Lx,Ly,d} \right) = CI\left( {m + Lx,d} \right)/CI\left( {Lx,d} \right)$ | (7) |
其中:
$CI = \left( {m + Lx,Ly,d,n} \right) = \Pr \left( {\left\| {X_{t - Lx}^{m + Lx} - X_{s - Lx}^{m + Lx}} \right\| < d,\left\| {Y_{t - Ly}^{Ly} - Y_{s - Ly}^{Ly}} \right\| < d} \right)$
$CI = \left( {Lx,Ly,d} \right) = \Pr \left( {\left\| {X_{t - Lx}^{m + Lx} - X_{s - Lx}^{m + Lx}} \right\| < d,\left\| {Y_{t - Ly}^{Ly} - Y_{s - Ly}^{Ly}} \right\| < d} \right)$
$CI = \left( {m + Lx,d} \right) = \Pr \left( {\left\| {X_{t - Lx}^{m + Lx} - X_{s - Lx}^{m + Lx}} \right\| < d} \right)$
$CI = \left( {Lx,d} \right) = \Pr \left( {\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d} \right)$
假定Xt、Yt是严格平稳同时要满足混合条件,基于原假设“Yt不是Xt的严格Granger原因”,Diks和Panchenko(2006)构造了渐进正态分布的T统计量,如式(8)所示:
| $T = \left[{\frac{{CI\left( {m + Lx,Ly,d,n} \right)}}{{CI\left( {Lx,Ly,d,n} \right)}} - \frac{{CI\left( {m + Lx,d,n} \right)}}{{CI\left( {Lx,d,n} \right)}}} \right] \sim N\left( {0,\frac{1}{{\sqrt m }}{\sigma ^2}\left( {m + Lx,Ly,d,n} \right)} \right)$ | (8) |
其中:n=T+1-m-max(Lx, Ly),σ2(·)是修正的检验统计量的渐进方差。根据式(8)中的统计量可依次对式(1)和式(2)VAR模型中的两个估计残差序列(ε1,t,ε2,t)做出检验。若Granger非因果的原假设被拒绝,则两个序列间就存在非线性因果关系。
(二)空间网络结构特征的刻画——社会网络分析。①社会网络分析(SNA)以“关系”作为基本分析单位,是一种针对“关系数据”的跨学科分析方法,其应用领域已经从社会学向经济学、管理学等领域拓展,并逐步成为一种新的研究范式(Scott,2013)。在社会网络分析中,整体网络结构特征通常利用网络密度、网络效率、网络关联度以及网络等级度进行刻画;而个体网络结构特征则通常利用度数中心度、接近中心度、中介中心度指标进行分析。本文将采用上述方法来揭示中国省际经济增长非线性溢出效应的联动网络结构特征。
① 限于篇幅,具体公式没有给出,有需要的读者可以参见刘军(2014)及其他相关文献。
(三)样本数据。本文采用中国29个省(自治区、直辖市,下同)作为样本,样本数据时期跨度为1978-2013年。由于重庆在1997年才成为直辖市,因此将重庆与四川合并,统称四川。另外,样本中不考虑西藏(数据缺失严重)、中国香港、中国澳门和中国台湾地区。本文涉及的数据包括分省GDP和年末总人口数,上述数据来自国家统计数据库及历年《中国统计年鉴》。其中,分省国内生产总值按照2005年不变价的指数进行处理。
三、中国经济增长的空间分布格局为了刻画中国经济增长的空间分布格局,本文首先基于ArcGIS10.0软件,分别以1978年和2013年为时间基点,采用自然断点(Natural Breaks Jenks),把相似性最大的数据分在同一级,差异性最大的数据分在不同级,根据我国各省经济增长水平(人均GDP)划分为经济不发达、经济欠发达、经济中等、经济次发达和经济发达五个类别,以直观展示我国省际时点特征的空间等级分布格局(图 1)。由图 1可见,中国经济增长存在显著的空间非均衡特征。进一步地,本文利用趋势分析工具(Trend Analysis Tool)对中国省际经济增长水平的空间分布趋势进行了可视化,如图 2所示。其中,图 2中每根竖线代表一个省人均GDP的值(高度)和位置。图中的数据点是竖线在东西向和南北向正交平面上的投影,将投影点进行拟合可以得到一条最佳拟合线,用它模拟了东西和南北方向上存在的趋势。
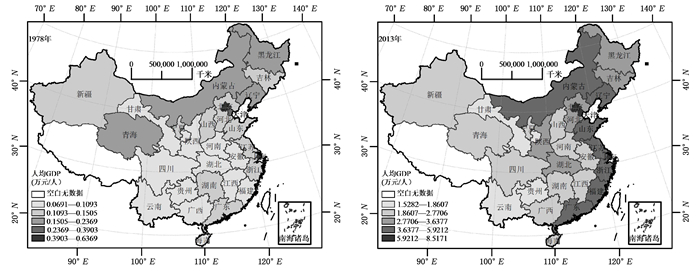
|
| 图 1 中国经济增长的空间格局 |
图 2显示,1978年我国省域经济增长水平的曲线,在东西方向上呈一条小弧“U”形曲线,投影线坐落在1格和2格间;南北方向上呈一条稍被拉平的“S”形曲线,范围也坐落在1格和2格间。这表明1978年我国省域经济增长水平在东西方向上,东部地区依次高于西部和中部地区;在南北方向上,东部地区依次高于东北部和南部地区。2013年我国省域经济增长水平的曲线,在东西方向上强化了“U”形曲线的右弧线,投影线坐落在了1格和4格间,南北方向上继续呈“S”形曲线,左峰也不断上升。经分析可知,1978-2013年我国经济增长水平呈现显著的空间非均衡分布格局。
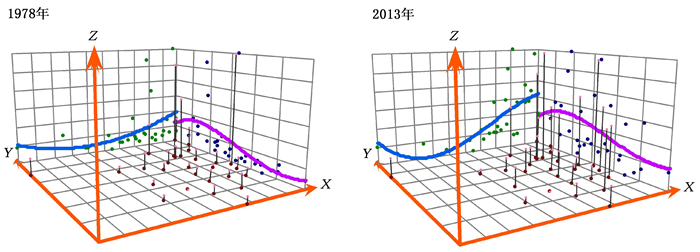
|
| 图 2 中国经济增长的空间趋势分析 注:X、Y正方向分别表示正东、正北。 |
Granger因果检验的前提是序列为平稳序列,我们采用Ng和Perron(2001)提出的单位根检验方法对29个省的人均GDP(取自然对数)序列进行平稳检验,检验结果表明所有序列均为I(1)过程,而其差分序列均显示为平稳过程。因此后文分析中我们将采用差分后的序列进行非线性Granger因果检验。为了考察经济增长的空间传导和溢出是否存在非线性趋势,我们采用BDS检验方法对省际经济增长的动态变化趋势进行非线性检验,结果显示地区间经济增长存在显著的非线性趋势。①
① 限于篇幅,单位根检验结果和BDS检验结果可向作者索取。
1.非线性Granger因果关系检验及空间网络可视化。传统的线性Granger因果检验对滞后阶数的选择极为敏感,通常可以采用VAR模型并通过AIC、SIC、LR、FPE和HQ五种准则选择最优滞后阶数。李敬等(2014)的最优滞后阶数选择按三种以上方法结果一致的原则确定,我们认为此种处理过于主观,必须加以重新思考。因此,相比线性Granger因果检验,尽管目前关于非线性Granger因果检验的最优滞后阶数选择并没有统一的规则(Diks和Panchenko,2006;Francis等,2010),但是却为我们更全面地认识省际经济增长的传导关系提供了新的思路。我们认为,如果所有滞后阶数下检验结果均接受“不存在非线性Granger因果关系”的原假设,则变量间一定不存在溢出关系。如果所有滞后阶数下检验结果至少有一个显著地拒绝“不存在非线性Granger因果关系”的原假设,则我们无法排除变量间存在溢出关系的可能,基于这种可能的溢出关系所形成的关联网络,我们可以将其定义为“最大可能性网络”(maximum likelihood network,以下简称ML-Network)。
根据VAR模型中的残差序列,并借鉴潘越(2008)的方法,我们选择滞后阶数Lx=Ly=1,2,3,带宽取1.5,对省际经济增长进行非线性Granger因果关系检验。②根据滞后1-3阶的检验结果,确定最大可能性空间关联关系并建立最大可能性关联关系矩阵,在此基础上,采用Netdraw对ML-Network进行可视化,由图 3可见,中国省际经济增长的空间关联确实呈现出复杂的、多线程的网络结构形态,没有任何一个省份能够“孤立”于整体网络。“不谋全局者,不能谋一域”,中国经济增长的空间网络结构要求我们要从全局的、整体的视角来实现区域协调发展。

|
| 图 3 中国省际经济增长的最大可能性空间关联网络 |
2.中国省际经济增长空间关联的整体网络结构特征。根据非线性Granger因果检验结果,借助社会网络分析范式,我们分别测算了ML-Network的实际关联关系总数、网络密度、网络等级度以及网络效率,表 1报告了具体结果。为了与已有研究进行对比,表 1也给出了李敬等(2014)的测度结果。图 4则直观地描述了我们与李敬等(2014)测度结果的差异。
| 网络 | 关联关系数 | 网络密度 | 网络关联度 | 网络等级度 | 网络效率 |
| 李敬等(2014) | 179 | 0.220 | 1 | 0.133 | 0.653 |
| ML-Network | 367 | 0.452 | 1 | 0.000 | 0.347 |

|
| 图 4 中国省际经济增长空间关联的整体网络结构特征 |
(1)关联关系总数与网络密度。在以29个省份为节点的空间关联网络中,节点之间最大可承载的单向溢出关系数共有812条。李敬等(2014)基于线性Granger因果检验得出的实际关联关系数为179,网络密度为0.220。本文基于非线性Granger因果检验得出的最大可能性关联关系数为367,网络密度达到0.452,超出李敬等(2014)网络密度的一倍以上。因此,采用线性Granger因果检验方法严重低估了中国省际经济增长的空间关联性。相比线性方法,在考虑非线性因素后中国省际经济增长更多的空间关联关系被识别出来,空间关联关系更为密切,整体网络结构也更为稳固。当然我们与李敬等(2014)之间的结论差异除了样本数据略有差别外,更多在于空间关联关系的识别方法,换言之,采用非线性Granger因果检验方法可以更加准确地揭示中国省际经济增长的空间关联,而且非线性Granger因果检验方法能够识别出更多可能的空间溢出渠道,这为当前及未来充分发挥区域经济增长的空间溢出效应,不断提升区域经济增长的空间协同效应提供了更多实证上的依据。
(2)网络关联性:网络关联度、网络等级度和网络效率。根据表 1的测度结果以及图 4,ML-Netwok的网络关联度为1,网络连通效果好,网络具有很好的通达性,省际存在普遍的空间溢出效应,这与李敬等(2014)的研究结论一致。ML-Netwok的网络等级度为0,而李敬等(2014)的网络等级度为0.133,这说明在基于非线性Granger因果检验方法所构建的最大可能性网络中,省际经济增长完全不存在等级结构,不同省份经济增长之间均有空间溢出的可能,这进一步为空间协同发展提供了实证依据。ML-Netwok的网络效率为0.347,远小于李敬等(2014)的0.653,这表明,基于非线性Granger因果检验方法下构建的最大可能性网络中,冗余连线更多,省际经济增长存在更多的多重叠加现象,网络更加稳定。
3.中国省际经济增长空间关联网络的个体中心性分析。表 2报告了在中国省际经济增长空间关联的ML-Network中不同省份个体的中心性测度结果,同样地,为了与已有研究对比,表 2也给出了李敬等(2014)的结果。
| 省份 | 李敬等(2014) | ML-Network | |||||||||
| 受益关系 | 溢出关系 | 关系总数 | 度数中心度 | 中间中心度 | 受益关系 | 溢出关系 | 关系总数 | 点度中心度 | 中间中心度 | 接近中心度 | |
| 注:李敬等(2014)未报告接近中心度,同时其样本包括西藏而不含海南;ML-Network中含有海南而不含西藏。 | |||||||||||
| 北 京 | 2 | 7 | 9 | 25.000 | 0.594 | 18 | 16 | 34 | 78.571 | 1.260 | 82.353 |
| 天 津 | 11 | 12 | 23 | 67.857 | 10.122 | 2 | 3 | 5 | 17.857 | 0.083 | 53.846 |
| 河 北 | 6 | 5 | 11 | 35.714 | 1.109 | 19 | 19 | 38 | 82.143 | 1.651 | 84.848 |
| 山 西 | 0 | 6 | 6 | 21.429 | 0.249 | 15 | 13 | 28 | 71.429 | 1.035 | 77.778 |
| 内蒙古 | 3 | 13 | 16 | 39.286 | 1.141 | 6 | 12 | 18 | 57.143 | 0.489 | 70.000 |
| 辽 宁 | 7 | 5 | 12 | 42.857 | 2.554 | 14 | 14 | 28 | 71.429 | 1.385 | 77.778 |
| 吉 林 | 7 | 11 | 18 | 57.143 | 4.970 | 19 | 9 | 28 | 75.000 | 1.046 | 80.000 |
| 黑龙江 | 4 | 6 | 10 | 32.143 | 0.823 | 7 | 18 | 25 | 71.429 | 1.446 | 77.778 |
| 上 海 | 7 | 3 | 10 | 28.571 | 0.957 | 9 | 1 | 10 | 35.714 | 0.271 | 60.870 |
| 江 苏 | 6 | 5 | 11 | 32.143 | 1.988 | 18 | 10 | 28 | 75.000 | 1.022 | 80.000 |
| 浙 江 | 7 | 3 | 10 | 32.143 | 2.207 | 22 | 7 | 29 | 78.571 | 1.104 | 82.353 |
| 安 徽 | 13 | 3 | 16 | 53.571 | 5.084 | 16 | 17 | 33 | 85.714 | 2.827 | 87.500 |
| 福 建 | 4 | 4 | 8 | 28.571 | 0.746 | 19 | 15 | 34 | 78.571 | 1.437 | 82.353 |
| 江 西 | 8 | 3 | 11 | 35.714 | 0.950 | 14 | 14 | 28 | 67.857 | 1.254 | 75.676 |
| 山 东 | 2 | 7 | 9 | 32.143 | 1.309 | 16 | 11 | 27 | 71.429 | 1.155 | 77.778 |
| 河 南 | 13 | 7 | 20 | 67.857 | 6.434 | 9 | 12 | 21 | 64.286 | 1.728 | 73.684 |
| 湖 北 | 9 | 7 | 16 | 39.286 | 1.162 | 16 | 19 | 35 | 82.143 | 1.362 | 84.848 |
| 湖 南 | 0 | 12 | 12 | 42.857 | 1.040 | 10 | 11 | 21 | 57.143 | 0.389 | 70.000 |
| 广 东 | 5 | 5 | 10 | 28.571 | 0.920 | 13 | 12 | 25 | 67.857 | 0.674 | 75.676 |
| 广 西 | 5 | 12 | 17 | 50.000 | 3.234 | 9 | 16 | 25 | 71.429 | 1.022 | 77.778 |
| 海 南 | - | - | - | - | - | 16 | 9 | 25 | 78.571 | 1.239 | 82.353 |
| 四 川 | 2 | 7 | 9 | 28.571 | 0.475 | 5 | 6 | 11 | 39.286 | 0.190 | 60.870 |
| 贵 州 | 3 | 13 | 16 | 50 | 4.861 | 15 | 13 | 28 | 78.571 | 2.381 | 82.353 |
| 云 南 | 5 | 5 | 10 | 32.143 | 1.235 | 10 | 21 | 31 | 85.714 | 1.941 | 87.500 |
| 西 藏 | 7 | 5 | 12 | 35.714 | 0.942 | - | - | - | - | - | - |
| 陕 西 | 10 | 2 | 12 | 42.857 | 1.731 | 13 | 17 | 30 | 82.143 | 1.735 | 84.848 |
| 甘 肃 | 10 | 4 | 14 | 50 | 3.710 | 14 | 13 | 27 | 67.857 | 1.179 | 75.676 |
| 青 海 | 11 | 6 | 17 | 50 | 3.761 | 8 | 20 | 28 | 75.000 | 2.082 | 80.000 |
| 宁 夏 | 12 | 12 | 24 | 39.286 | 2.119 | 12 | 12 | 24 | 60.714 | 1.541 | 71.795 |
| 新 疆 | 2 | 2 | 4 | 14.286 | 0.243 | 3 | 7 | 10 | 35.714 | 0.258 | 58.333 |
(1)溢出关系、受益关系、关联关系总数和净溢出关系。根据表 2结果,发出溢出关系排名前五位的省份依次是云南、青海、河北、湖北和黑龙江,而上海、天津、四川、浙江、新疆等省份发出的溢出关系较少。从受益关系看,受益关系排在前列的省份有浙江、吉林、河北、北京、江苏等,而受益关系较少的省份是天津、新疆、四川、内蒙古、黑龙江等。从关联关系总数(溢出关系与受益关系之和)看,河北、北京、福建、云南、陕西在ML-Network中的关联关系总数均在30以上(含30);而天津、新疆、上海在ML-Network中的关联关系则较少,均在10以下(含10)。从净溢出关系(溢出关系数与受益关系数之差)看(如图 5),青海、云南、黑龙江、广西、内蒙古、陕西、新疆、河南、湖北、湖南、天津、安徽和四川13个省份的净溢出关系数为正,因此总体效应为溢出;浙江、吉林、上海、江苏、海南、山东、福建、北京、山西、贵州、广东和甘肃12个省份的净溢出关系数为负,因此总体是受溢出的。另外,河北、辽宁、江西和宁夏4个省份的溢出关系等于受益关系。我们的结论与李敬等(2014)的结果存在较大差异,这主要是受空间关联关系识别方法的影响。因此,若按照线性Granger因果检验方法,可能对处于空间关联网络中不同省份的角色和地位做出错误的判断。以北京为例,在李敬等(2014)的研究中,北京的溢出关系为7,受益关系为2,因此北京总体上是溢出的;而在我们的ML-Network中,北京的溢出关系是16,受益关系是18,总体上是受益的。北京作为我国的经济、政治和文化中心,应当更多地扮演溢出角色而非受益角色,因此基于线性Granger因果检验的研究可能存在一定偏误。
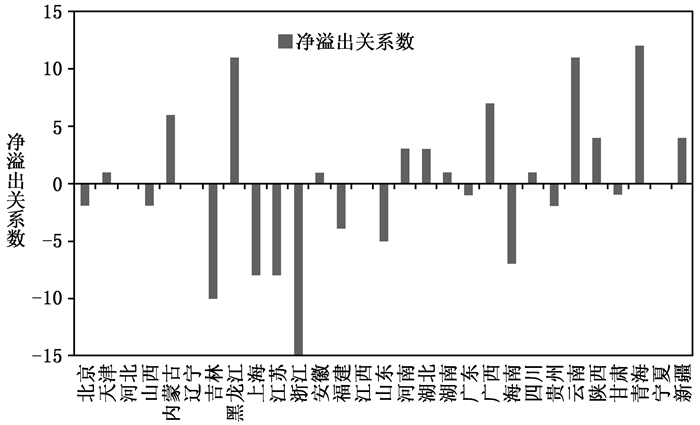
|
| 图 5 不同省份的空间关联关系 |
(2)度数中心度、中间中心度、接近中心度。首先是度数中心度。根据表 2,在ML-Network中,安徽、云南、河北、湖北、陕西的度数中心度排名前5位,说明这些省份在省际经济增长空间关联网络中与其他省份发生的关系数较多,处于网络的核心位置。天津、新疆的度数中心度排名垫底,其经济增长与其他省份之间的关联关系较少,需要通过提高与其他省份的关联程度来增加经济增长的溢出管道。在李敬等(2014)的研究中,天津、河南、吉林、安徽和广西的度数中心度为前五。由与李敬等(2014)的比较分析可见,处于网络中心位置的省份发生了较大变动。其中,安徽的度数中心度由53.571变为85.714,由排名第4变为排名第1;云南由排名第22变为第2,河北由第15变为第3,湖北由第13变为第4,陕西由第11变为第5。特别地,天津的度数中心度由排名1变为了全国倒数第1。上述结果进一步表明,基于线性Granger因果检验方法识别的省际经济增长空间关联关系并不能准确揭示不同省份在网络中的地位和角色,可能对政策产生一定的误导。其次是中间中心度。同样根据表 2,在ML-Network中,安徽、贵州、青海的中间中心度排名全国前3,在经济增长空间关联网络中处于核心地位并发挥重要的“桥梁”作用。而中间中心度排名靠后的省份依次是天津、四川和新疆,难以对网络中的其他省份起到控制和支配作用。在李敬等(2014)的研究中,中间中心度处于前3名的是天津、河南、安徽。另外,通过对比我们还发现,北京、上海两个直辖市在ML-Network中的中间中心度与李敬等(2014)相比明显缩小,而山东、广东在ML-Network中的中间中心度明显扩大。最后是接近中心度。在ML-Network中,安徽、云南、湖北、河北的接近中心度排名靠前,这表明这些省份在经济增长空间关联网络中不易受其他省份的影响,在网络中扮演着“中心行动者”的角色。而天津、新疆、四川等省份的接近中心度排名靠后,其与其他省份存在较弱的联系,在经济增长空间关联网络中扮演着“边缘行动者”的角色。
3.块模型分析。本文采用Concor方法(Convergent Correlation),选择2为最大的分割深度,集中标准设定为0.2,将29个网络节点划分为四个板块,板块的划分结果见表 3。
| 板块 | 成员 | 成员个数 |
| 第一板块 | 北京、河南、河北、山西、安徽、福建、宁夏、新疆、贵州、青海 | 10 |
| 第二板块 | 上海、山东、辽宁、吉林、新疆、湖北、甘肃、云南、海南 | 8 |
| 第三板块 | 广东、浙江、湖南、四川、天津、广西 | 6 |
| 第四板块 | 江苏、内蒙古、江西、黑龙江、陕西 | 5 |
表 4报告了四个板块的密度矩阵,根据前文测算,中国省际经济增长空间关联ML-Network的网络密度为0.452。本文将ML-Network中板块密度大于整体网络密度的情形赋值为1,将板块网络密度小于整体网络密度的情形赋值为0,进而把板块网络密度矩阵转化为像矩阵,并按照α密度准则得出了板块像矩阵的可视化关联图,见图 6。根据图 6,ML-Network中的第一板块为“净溢出板块”,扮演了“发动机”的角色,它将经济增长的动能传递给了扮演“中介人”角色的第四板块,即第四板块发挥了明显的桥梁和枢纽作用。第四板块又将经济增长的动能传递给扮演“双向溢出”角色的第二板块和扮演“净受益”角色的第三板块。然而,第三板块与第一板块、第二板块之间不发生传导溢出关系。整体上来说,网络中各板块的传递关系具有明显的“梯度”溢出特征。同时,依据ML-Network中板块之间的关系,需要加强第三板块内的省份与第一板块、第二板块内省份之间的联系与互动,这一结论对中国区域经济发展战略相关政策的制定提供了重要的决策依据与支持。
| 板块 | 第一板块 | 第二板块 | 第三板块 | 第四板块 |
| 第一板块 | 0.533 | 0.575 | 0.400 | 0.520 |
| 第二板块 | 0.512 | 0.482 | 0.250 | 0.425 |
| 第三板块 | 0.383 | 0.313 | 0.233 | 0.333 |
| 第四板块 | 0.440 | 0.650 | 0.600 | 0.250 |
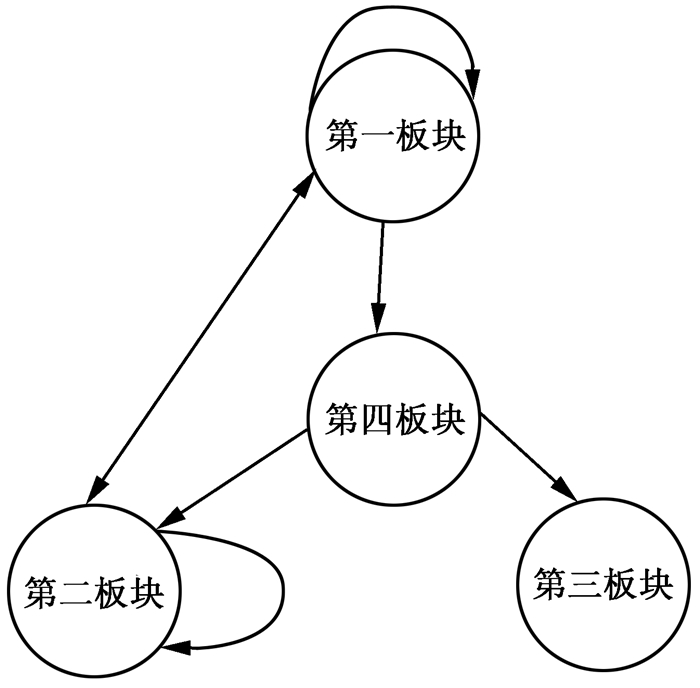
|
| 图 6 不同板块在ML-Network中的相互关系 |
本文基于1978-2013年中国大陆分省数据,利用非线性Granger因果检验方法确定省际经济增长的空间关联关系并建立了ML-Network,在此基础上利用社会网络分析方法对省际经济增长空间关联的网络结构进行了实证考察。研究发现:(1)线性Granger因果检验方法低估了中国省际经济增长的空间关联性,而采用非线性Granger因果检验方法不仅可以揭示出更多的空间关联关系,而且能够识别出更多可能的空间溢出管道,这为提升中国经济增长的空间协同效应提供了更多实证上的支持。(2)中国省际经济增长从整体上呈现出更紧密的、更稳定的网络结构形态,在中国省际经济增长空间关联的ML-Network中,没有任何一个省份能够“孤立”于整体网络。“不谋全局者,不能谋一域”,我们必须从全局的、整体的视角协调区域经济发展。基于上述结论,我们建议如下:
第一,要更加重视我国经济增长的空间非均衡问题,全面认识经济增长的空间关联关系及其网络结构特征。为防止地区差距的不断扩大,继续推动西部大开发、东北振兴和中部崛起的区域协调政策以及落实好“京津冀一体化”、“长江经济带”等新的区域发展战略的实施。省际经济增长存在较强的空间关联性,而且这种关联不是简单的单个省份对单个省份(点对点)的关系,而是呈现复杂的网络结构形态,使各个省份的经济增长不仅取决于自身而且也与其他省份存在密切联系,这无疑为经济发展政策的制定和顺利实施带来了严峻挑战和机遇。因此,要通过宏观调控和市场机制为经济跨区域交流和空间优化配置创造更多有利条件。第二,不断调整和优化经济增长的空间关联网络结构,提高经济增长的空间配置效率,以此更好地实现空间协同发展。不仅要重视单纯地理意义上的近邻效应,更要重视经济增长的空间关联关系所呈现出的复杂的网络结构形态,进而从地理近邻效应和网络效应两个维度为我国跨区域协同发展机制的构建提供新的指导策略。而在经济政策的制定和实施过程中,不仅要考虑“属性数据”(即数量)的表现,也要重视经济增长的空间联动效应(结构),逐步形成“数量—结构”驱动型的协同发展思路,推动经济政策从“局部”转向“整体”,从“点”转向“面”,实现经济政策的有效转向。第三,不谋全局者,不足谋一域。中国省际经济增长的空间传导及其联动网络表明,面对各省经济增长的空间非均衡问题,在一个省际联片发展区域中,没有一个省份可以独善其身,建立区域协同发展机制是缩小地区经济差距、实现区域协调发展的必然选择。坚持区域协同发展,就要从整体和全局上把握,以协同的理念持续推动经济社会发展,提升发展的整体效能。这就促使我们要协同推进地区间战略互信、经贸合作、人文交流,提高边省经济合作区、跨省经济合作区的发展水平,努力形成深度融合的互利合作格局。第四,探寻更多的空间溢出渠道,发挥经济增长不同板块的不同功能,促进地区间的空间溢出效应,进而最终实现各区域的空间协同发展。这就要求在协同发展中拓宽发展空间,在加强薄弱领域中增强发展后劲,在新的时期需要不断塑造要素流动有序自由、主体功能约束有效、基本公共服务均等、资源环境可承载的区域协同发展新格局。根据各地的实际情况,统筹兼顾、因地制宜地把协调发展理念落到实处,使不同区域发展的动能聚合成整体发展的势能,形成更有利于解决发展问题的总体趋势,开创各地区经济社会发展相互促进、区域协同推进的良好发展局面。
| [1] | 陈雄兵,张宗成. 再议 Granger 因果检验[J]. 数量经济技术经济研究,2008,(1):154-160. |
| [2] | 陈秀山,张可云. 区域经济理论[M]. 北京:商务印书馆,2005. |
| [3] | 李国平,吴爱芝,孙铁山. 中国区域空间结构研究的回顾及展望[J]. 经济地理,2012,(4):6-11. |
| [4] | 李敬,陈澍,万广华,等. 中国区域经济增长的空间关联及其解释——基于网络分析方法[J]. 经济研究,2014,(11):4-16. |
| [5] | 刘华军,张耀,孙亚男. 中国区域发展的空间网络结构及其时滞变化——基于DLI指数的分析[J]. 中国人口科学,2015,(4):60-71. |
| [6] | 刘华军,张耀,孙亚男. 中国区域发展的空间网络结构及其影响因素——基于中国2000-2013年省际地区发展与民生指数[J]. 经济评论,2015,(5):59-69. |
| [7] | 刘军. 整体网分析[M]. 上海:格致出版社、上海人民出版社,2014. |
| [8] | 潘文卿. 中国区域关联与经济增长空间溢出效应[J]. 经济研究,2012,(1):54-65. |
| [9] | Francis B B, Mougoué M, Panchenko V. Is there a symmetric nonlinear causal relationship between large and small firms?[J]. Journal of Empirical Finance, 2010, 17(1): 23-38. |
| [10] | Groenewold N, Lee G, Chen A. Inter-regional spillover in China: The importance of common shocks and the definition of the regions [J]. China Economic Review, 2008, 19(1): 32-52. |
| [11] | Groenewold N, Lee G, Chen A. Regional output spillover in China: Estimates from a VAR model[J]. Regional Science, 2007, 86(1): 101-122. |
| [12] | Ng S,Perron P. Lag length selection and the construction of unit root tests with good size and power [J]. Econometrica, 2001, 69(11): 1529-1554. |
| [13] | Scott J. Social network analysis: A handbook (3rd edition) [M]. New York:Sage Publication, 2013. |
| [14] | Wooldrige J M. Introductory econometrics:A modern approach (5th edition) [M]. South-Western Cengage Learning, 2012. |
| [15] | Ying L G. Understanding China's recent growth experience: A spatial econometric perspective [J]. Annals of Regional Science, 2003, 37(4), 613-628. |
 2016, Vol. 42
2016, Vol. 42


