文章信息
- 谢呈阳, 胡汉辉, 周海波
- Xie Chengyang, Hu Hanhui, Zhou Haibo
- 新型城镇化背景下“产城融合”的内在机理与作用路径
- Principles and Paths of the City-industry Integration Development against the Background of a New Kind of Urbanization
- 财经研究, 2016, 42(1): 72-82
- Journal of Finance and Economics, 2016, 42(1): 72-82.
-
文章历史
- 收稿日期:2015-06-03
一、引言
“产城融合”发展理念是针对中国高速城镇化进程中出现的产业功能与城市功能分离的现象提出的,其含义是城市发展要以产业为(经济)基础,产业发展要以城市为(空间)载体,城市化与产业化要有相对应的匹配度(杨立勋和姜增明,2013)。2014年3月,《国家新型城镇化规划(2014-2020年)》(以下简称《规划》)出台,“产城融合”再一次成为新型城镇化发展的主导思路。①在这样的大背景下,深入思考“产城融合”的内在机理与作用路径具有理论和现实意义。
①2014年3月颁布的《国家新型城镇化规划(2014-2020)》中提出将“产城融合”放在突出位置
“新型城镇化”中的“新”体现在“以人为本”被提高到前所未有的高度,这意味着对“产城融合”的理解需要从过去的“功能导向”转向现在的“人本导向”,但目前鲜有以此为切入视角的讨论。即使是单纯着眼于“产城融合”的研究也多是基于单一案例的经验总结,技术路线大致相同:或者通过回顾某个地区的发展历程来总结措施和成功经验,或者通过对比区域实施“产城融合”前后经济指标的变化来说明“产城融合”的重要性(蒋华东,2012;孔翔和杨帆,2013),几乎没有深入原理层的研究。
鉴于此,本文结合新型城镇化背景,首先纳入“人”的需求,对“产城融合”的概念提出新解;然后基于概念解读,构建理论模型,揭示“产”、“城”之间的协同路径和经济学原理;最后以江苏省65个县(区)10年的经济数据为样本,实证检验理论模型,并得出附加结论。
本文可能的贡献体现在:第一,通过“概念抽象-模型推导-数据检验”的科学过程,论证了“产城融合”能够同时提高“人”的效用和繁荣经济,为新型城镇化建设中“产城融合”战略的推进提供了理论依据;第二,系统地阐明了新型城镇化背景下“产城融合”的内在机理和作用路径;第三,附加结论能够反映目前“产城融合”中存在的问题,对中国诸多地区的新型城镇化建设具有参考价值。
二、新型城镇化背景下“产城融合”的概念解读新型城镇化的“人本导向”并未改变“产城融合”概念中“产”的含义,“产城融合”提出时“产”主要指的是工业。结合《规划》中多次指出的要“工业化和城镇化良性互动”,本文将“产”理解为以工业为主体的产业。
新型城镇化的最终目的是提高生活在“城”中的“人”的效用水平,而以此出发,“城”就不能再仅仅理解为“城市”、“城镇”或者“园区”这样的产业发展空间载体。在马斯洛需求框架下,“人”的需求主要包括:满足生理需求的食品、住宅;满足安全需求的医疗;满足社交需求的娱乐;满足尊重需求的就业、高档消费;满足自我实现需求的教育、培训等。不难发现,“城”满足“人”需求的主要手段是“城市功能”结合“城”所包含的空间含义,本文更倾向于将其理解为在“人”聚集的地理范围内满足“人”不同层次需求的城市功能。
从“人”的视角出发,“产”与“城”需要融合的原因至少有三点:第一,在经济理论中“人”通常被抽象成劳动力,劳动力是“产”的重要投入要素,因此其与“产”在地域上具有天然的不可割裂性;第二,与普通生产要素仅需要提供储存空间不同,劳动力存在多层面的需求,因此其与“城”必然存在千丝万缕的联系;第三,城市功能的获得在很大程度上来自作为“产”之一的服务业。与工业产品相比,服务具有无形性、不可储存性、生产与消费同时性三大特征(Browning和Singelman,1975)。尽管在现代信息和通讯技术的影响下,上述三个特点都已受到不同程度的挑战和质疑,但改变却有限,大多数服务活动尤其是消费服务仍受到明显的时空限制(江小涓,2011)。因此,服务业很难对“人”实现“跨区域”供给,即“城”的功能无法作用于不在其地理范围内的“人”。
同样从“人”的视角出发,“产”与“城”之间能够相互促进:第一,“城”能够通过提高“人”的效用水平来吸引高质量的劳动力,进而提升地区的产业发展水平。我们在对多个工业镇(村)的走访调研中发现,制约当地产业升级的最大问题往往并非资金或技术,而是长期只注重工业发展、忽略生活要素配套的“产”、“城”脱节发展模式所带来的商贸、教育、医疗等服务的缺乏。劳动力(尤其是高质量劳动力)因需求无法被满足而大量流失,导致产业升级陷入瓶颈。第二,“产”能够通过促进“人”的集聚,为“城”的繁荣提供必要前提。如上文所述,城市功能的获得主要来自服务业,而由于生产与消费的同时性,需求规模是制约服务业发展的根本条件,只有大量消费者和经济组织集中在一起,才可能提供服务产业化所需的足够大的市场需求(Hill,1977)。工业发展能够引致劳动力集聚(这在中国伴随城镇化的高速工业化发展中已得到体现),为作为城市功能载体的服务业的催生提供良好环境。
综上所述,新型城镇化背景下的“产城融合”应该是“产业”、“人”和“城市功能”三者的融合。在“以人为本”的指导思想下,“产城融合”的最终目的是在提高“人”的效用水平的前提下,实现产业与城市发展的共同繁荣。而基于“人”这一视角的讨论又表明,“人”是“产”、“城”之间有效互动和融合上升的关键连接点。下文将通过经济学模型来论证这一过程,并详细阐述其内在机理和作用路径。
三、理论模型(一)思路和框架
1.基本要素。我们抽象出“产城融合”的以下关键要素:第一,“劳动力”:即“人”,既是产业发展的投入要素,又是城市功能的直接需求方;第二,“工业”:“产”的主要组成部分;第三,“服务业”:“城市功能”的主要供给载体,也是“产”的组成部分;第四,“住宅”:属于服务业,但存在“刚性需求”(范剑勇和邵挺,2011)的特殊性,我们将其单列,以便于下文分析。
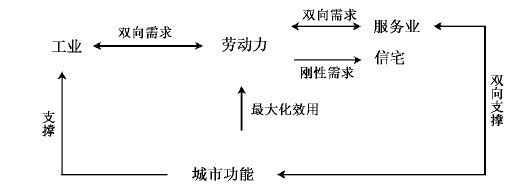
2.整体框架。为了将抽象后的要素纳入一个分析框架,本文借鉴了将劳动力、农业和工业纳入同一框架的核心-边缘模型(Krugman,1991)。本文模型与核心-边缘模型的区别在于去掉了农业部门,加入了住宅①和服务业部门。基本理论框架见图1。
①Helpman(1998)等学者已经论证了这样的改变不会影响模型的稳健性。
|
| 图 1 “产城融合”的理论模型框架 |
3.分析思路。本文将以劳动力效用最大化(“产城融合”的目的)为出发点来构建基本等式,然后利用均衡条件来阐述“融合”过程中“产”、“城”间基于上述四大关键要素的作用路径。需要说明的是,工业与服务业的繁荣均可看做产业的繁荣,而由于“城市功能”的载体是服务业,在下文的分析中,服务业繁荣程度等同于城市功能完备程度。本文将沿用核心-边缘模型的三大基石:D-S垄断竞争假设、CES效用函数和“冰山贸易成本”,以及由这些条件得到的推论。
(二)基本等式假设存在两个地区(记为1和2),每个地区的生产部门都由工业品部门和服务部门组成。劳动力根据自身收入通过消费地区间自由贸易的工业品以及不能自由贸易的服务产品和住宅来实现效用最大化,假设劳动力的效用函数为U=CMaCSbCHC,其中a、b和c分别表示劳动力在工业品、服务和住房上的花费占收入的份额,a+b+c=1。劳动力不会轻易在行业间流动,因此工业工资和服务业工资可以存在差异。
设定商品在地区间的运输费用为T,整个社会的总劳动力为L,从事工业品生产的劳动力份额为μ,则从事服务业的为1-μ;设定地区1从事工业品生产的劳动力占从事工业品生产的总劳动力的比例为λ,从事服务业的劳动力占从事服务业的总劳动力的比例为γ,则地区2相对应的比例分别为1-λ和1-γ。设定服务产品间的替代弹性为εS,工业品间的替代弹性为εM,W表示工资率,下标M和S分别表示工业部门和服务业部门。地区1和地区2的总收入可以分别表示为:
基本等式1:Y1=μλW1M+(1-μ)γW1S
基本等式2:Y2=μ(1-λ)W2M+(1-μ)(1-γ)W1S
我们首先求解两个地区工业品和服务的价格指数。假设代表性厂商i的生产函数为:
| ${l_i} = \alpha + \beta {x_i}$ | (1) |
| ${p_i} = \left[ {{\varepsilon _M}/\left( {{\varepsilon _M} - 1} \right)} \right]\beta {w_i}$ | (2) |
地区工业品价格指数取决于两部分:第一,在本地销售的由本地生产的工业品价格;第二,在本地销售的附加运输成本T的外地生产的商品价格。据此,两个地区的工业品价格指数分别为:
基本等式3:I1M=[λWM1M1-εM+1-λW2MTM1-εM]1/(1-εM)
基本等式4:I2M=[λW1MTM1-ε+1-λW2M1-εM]1/(1-εM)
由于服务难以跨地区交易,设定其运输成本无穷大,两个地区服务品价格指数分别为:
基本等式5:I1S=[γWS1-ε1S]1/(1-εS)
基本等式6:I2S=[(1-γ)WS1-ε2S]1/(1-εS)
我们接下来求解两个地区工业部门和服务业部门的工资率。工资率取决于厂商利润为0时的产出量和地区劳动力效用最大化时对工业品的需求量。以地区1的工业部门为例,劳动力效用最大化时有aY1的收入用于消费工业品。地区1代表性厂商i的均衡利润为0,则根据(2)式,产量为:
| ${x_i} = \alpha \left( {{\varepsilon _M} - 1} \right)/\beta $ | (3) |
地区1的劳动力在预算约束下通过消费不同的工业品i(价格为pi)实现效用最大化:
| ${\text{Max}}{C_M} = {\sum\limits_1^N {\left( {{c_i}^{\left( {{\varepsilon _M} - 1} \right)/{\varepsilon _M}}} \right)} ^{{\varepsilon _M}/\left( {{\varepsilon _M} - 1} \right)}}{\text{s}}{\text{.t}}{\text{.}}\sum\limits_1^N {{p_i}{x_i} = a{Y_1}} $ |
采用拉格朗日乘数法求得如下的最优解:
| ${c_i} = {p_i}^{ - {\varepsilon _M}}{I^{{\varepsilon _M} - 1}}a{Y_1}$ | (4) |
厂商面临的需求来自地区1和地区2,由于地区2消费地区1的产品时,劳动力面临的是附加了运输费用的价格,需求量会有一定程度的减少,为(piT)-εMIεM-12MaY2。
市场在厂商的产量与劳动力的需求相等时达到均衡,根据这一条件,我们有:
| $\alpha \left( {{\varepsilon _M} - 1} \right)/\beta = a\left[ {{p_i}^{ - {\varepsilon _M}}I_{1M}^{{\varepsilon _M} - 1}{Y_1} + {{\left( {{p_i}T} \right)}^{ - {\varepsilon _M}}}I_{2M}^{{\varepsilon _M} - 1}{Y_2}} \right]$ | (5) |
将(2)式代入(5)式可得:
| ${w_i} = {\left( {I_{1M}^{{\varepsilon _M} - 1}{Y_1} + I_{2M}^{{\varepsilon _M} - 1}{T^{ - {\varepsilon _M}}}{Y_2}} \right)^{1/{\varepsilon _M}}}$ |
据此,地区1和地区2工业部门的工资率可表示为:
| $\begin{gathered} 基本等式7:{W_{1M}} = {\left( {I_{1M}^{{\varepsilon _M} - 1}{Y_1} + I_{2M}^{{\varepsilon _M} - 1}{T^{ - {\varepsilon _M}}}{Y_2}} \right)^{1/{\varepsilon _M}}} \hfill \\ 基本等式8:{W_{2M}} = {\left( {I_{2M}^{{\varepsilon _M} - 1}{Y_2} + I_{1M}^{{\varepsilon _M} - 1}{T^{ - {\varepsilon _M}}}{Y_1}} \right)^{1/{\varepsilon _M}}} \hfill \\ \end{gathered} $ |
同理,两个地区服务业部门的工资率可表示为:
| $\begin{gathered} 基本等式9{W_{1S}} = {\left( {{Y_1}I_{1s}^{{\varepsilon _s} - 1}} \right)^{1/{\varepsilon _s}}} \hfill \\ 基本等式10{W_{2S}} = {\left( {{Y_2}I_{2s}^{{\varepsilon _s} - 1}} \right)^{1/{\varepsilon _s}}} \hfill \\ \end{gathered} $ |
两个地区实际工资率相等(此时两个地区劳动力效用相等)时模型达到均衡,可表述为:
| $\frac{{{W_{1M}}}}{{I_{1M}^aI_{1S}^bI_{1H}^c}} = \frac{{{W_{2M}}}}{{I_{2M}^aI_{2S}^bI_{2H}^c}},\frac{{{W_{1S}}}}{{I_{1M}^aI_{1S}^bI_{1H}^c}} = \frac{{{W_{2S}}}}{{I_{2M}^aI_{2S}^bI_{2H}^c}}$ | (6) |
其中,I1H和I2H分别表示地区1和地区2的房价指数,可衡量地区住宅市场的繁荣程度。
由于两个地区劳动力的分布形态即为产业的分布形态(Krugman,1991),设两个地区工业和服务业的比例分别为$\frac{{{N_{1M}}}}{{{N_{2M}}}}和\frac{{{N_{1S}}}}{{{N_{2S}}}}$,则有:$\frac{{{N_{1M}}}}{{{N_{2M}}}} = \frac{{{L_{1M}}}}{{{L_{2M}}}} = \frac{\lambda }{{1 - \lambda }},\frac{{{N_{1S}}}}{{{N_{2S}}}} = \frac{{{L_{1S}}}}{{{L_{2S}}}} = \frac{\gamma }{{1 - \gamma }}$。
四、理论分析根据研究思路,分析由均衡点展开。对于工业部门,我们可得:
| $\begin{gathered} \frac{{{W_{1M}}}}{{{W_{2M}}}} = {\left[ {\frac{{\lambda W_{1M}^{1 - {\varepsilon _M}} + \left( {1 - \lambda } \right){{\left( {{W_{2M}}T} \right)}^{1 - {\varepsilon _M}}}}}{{\lambda {{\left( {{W_{1M}}T} \right)}^{1 - {\varepsilon _M}}} + \left( {1 - \lambda } \right){{\left( {{W_{2M}}} \right)}^{\left( {1 - {\varepsilon _M}} \right)}}}}} \right]^{ - a/\left( {1 - {\varepsilon _M}} \right)}} \hfill \\ {\left[ {\frac{{\gamma W_{1S}^{1 - {\varepsilon _S}}}}{{\left( {1 - \gamma } \right)W_{2S}^{1 - {\varepsilon _S}}}}} \right]^{ - b/\left( {1 - {\varepsilon _S}} \right)}}{\left[ {\frac{{{I_{1H}}}}{{{I_{2H}}}}} \right]^{ - c}} \hfill \\ \end{gathered} $ | (7) |
令$\frac{a}{{1 - {\varepsilon _M}}} = {\rho _M},\frac{{ - b}}{{1 - {\varepsilon _S}}} = {\rho _S},F = {T^{1 - {\varepsilon _M}}}$。由于1-εM < 0,F与T负相关,可看作贸易自由度,由此可得:
| $\begin{gathered} {\left[ {\frac{{\lambda W_{1M}^{1 - {\varepsilon _M}} + \left( {1 - \lambda } \right){{\left( {{W_{2M}}T} \right)}^{1 - {\varepsilon _M}}}}}{{\lambda {{\left( {{W_{1M}}T} \right)}^{1 - {\varepsilon _M}}} + \left( {1 - \lambda } \right){{\left( {{W_{2M}}} \right)}^{\left( {1 - {\varepsilon _M}} \right)}}}}} \right]^{ - a/\left( {1 - {\varepsilon _M}} \right)}} = \hfill \\ {\left[ {\frac{{\frac{\lambda }{{\left( {1 - \lambda } \right)}}{{\left( {\frac{{{W_{1M}}}}{{{W_{2M}}}}} \right)}^{1 - {\varepsilon _M}}}F}}{{\frac{\lambda }{{\left( {1 - \lambda } \right)}}{{\left( {\frac{{{W_{1M}}}}{{{W_{2M}}}}} \right)}^{1 - {\varepsilon _M}}}F + 1}}} \right]^{ - {\rho _M}}} \hfill \\ \end{gathered} $ |
对上式分别在$\frac{\lambda }{{1 - \lambda }} = 0$和$\frac{{{W_{1M}}}}{{{W_{2M}}}} = 1$处进行二元泰勒展开,近似值代入(7)式,并两边取对数可得:$\begin{gathered} \ln \frac{{{W_{1M}}}}{{{W_{2M}}}} = - {\rho _M}\ln F + \ln \left[ {1 - \frac{{{\rho _M}}}{F}\left( {1 - {F^2}} \right)\frac{\lambda }{{1 - \lambda }}} \right] \hfill \\ - b\ln \frac{{{W_{1S}}}}{{{W_{2S}}}} + {\rho _S}\ln \frac{\lambda }{{1 - \lambda }} - c\ln \frac{{{I_{1H}}}}{{{I_{2H}}}} \hfill \\ \end{gathered} $。
将$n\left[ {1 - \frac{{{\rho _M}}}{F}\left( {1 - {F^2}} \right)\frac{\lambda }{{1 - \lambda }}} \right]$在${\frac{\lambda }{{1 - \lambda }}}$处进行一元泰勒展开,并简化整理可得:
| $\begin{gathered} \frac{\lambda }{{1 - \lambda }} = \frac{{ - F{\rho _M}}}{{\left( {1 - {F^2}} \right){\rho _M}}}\ln F - \frac{{ - Fb}}{{\left( {1 - {F^2}} \right){\rho _M}}}\ln \frac{{{W_{1S}}}}{{{W_{2S}}}} - \hfill \\ \frac{F}{{\left( {1 - {F^2}} \right){\rho _M}}}\ln \frac{{{W_{1M}}}}{{{W_{2M}}}} \hfill \\ + \frac{{ - F{\rho _S}}}{{\left( {1 - {F^2}} \right){\rho _M}}}\ln \frac{\gamma }{{1 - \gamma }} - \frac{{ - {F_C}}}{{\left( {1 - {F^2}} \right){\rho _M}}}\ln \frac{{{I_{1H}}}}{{{I_{2H}}}} \hfill \\ \end{gathered} $ | (8) |
根据设定,我们有εM>1,εS>1,ρM>0,ρS>0,0 < F < 1。根据(8)式,我们得到以下结论:在两个地区相对工资(名义工资)和运输成本一定的情况下,城市功能的繁荣可以促进产业的繁荣(a),但住宅市场的繁荣却会对工业产生挤出效应(b)。
同理分析两个地区服务业部门的均衡点可得:
| $\ln \frac{\gamma }{{1 - \gamma }} = \frac{{{\rho _M}}}{{{\rho _S}}}\ln F + \frac{{{\rho _M}\left( {1 - {F^2}} \right)}}{{F{\rho _S}}}\frac{\lambda }{{1 - \lambda }} + \ln \frac{{{W_{1S}}}}{{{W_{2S}}}} + \frac{c}{{{\rho _s}}}\ln \frac{{{I_{1H}}}}{{{I_{2H}}}}$ | (9) |
根据(9)式,两个地区相对工资(名义工资)和运输成本一定时,工业的繁荣可以促进城市功能的完备(c),住宅市场的繁荣对城市功能的完备(服务业繁荣)也起到正向作用(d)。同时,由于服务业与工业的比值一般被用来衡量地区产业结构,综合结论b和d,“产城融合”后住宅市场的繁荣会推动地区产业结构升级。
(一)“城”促进“产”的作用机理与路径(a)“城”(以服务业为载体)对“产”(以工业为主体)的作用路径可基于模型等式做出以下描述:城市功能完备程度的上升意味着服务业劳动力和总产出的增加,这会带动地区总收入的上升和对工业品需求量的增加。根据供求原理,在工业品短期供给不变的情况下,工业品价格会上升。以地区1为例,根据基本等式7,地区1服务业的繁荣不会影响地区2,但会同时提高I1M和Y1,从而引致地区1工业劳动力的名义工资率上升。由于规模报酬递增,厂商成本下降,而社会总需求却会随工业劳动力的流入进一步增加,这将引致地区1的工业繁荣程度上升。
(二)“产”促进“城”的作用机理与路径(c)“产”对“城”的作用路径与“城”对“产”的作用路径类似:工业的繁荣意味着工业产出和工业劳动力的增加,这将引致地区收入和对服务的需求增加。在服务短期供给不变的情况下,服务价格上升。以地区1为例,由基本等式9可知,服务业名义工资率仅取决于本地服务价格和本地社会总收入,因此工业的繁荣将引致服务业名义工资率上升。在短期内,名义工资率的上升将吸引更多的劳动力流入该地区服务业,对服务的需求进一步增加,在规模报酬递增的作用下,厂商成本下降,这将在长期引致地区1服务业的繁荣程度和以其为载体的城市功能完备程度上升。
(三)地区产业结构的升级路径(b和d)单从基本等式无法确切地给出住宅市场对地区产业结构的作用路径,但从劳动力入手却可以对这一路径进行分析:产业繁荣以劳动力流入为前提,而劳动力流入意味着住宅需求增加和住宅价格上涨。从短期看,住宅价格上涨对劳动力产生了挤出效应,但由于服务业具有“生产与消费的同时性”特征,其对本地消费群体的依赖超过工业,因此住宅价格对工业部门的挤出效应较服务业部门更甚,表现为服务业在地区产业中所占比例上升。随后,由于劳动力的流出,住宅价格下跌,地区实际工资率上升,再次带来劳动力流入,如此循环往复,长期会推动地区产业结构升级。
至此,我们可以将“产城融合”的过程做完整的描述:初始时,以劳动力为连接点,地区产业因工业与服务业相互促进而更加繁荣,城市功能因其载体服务业的繁荣而更加完备,劳动力效用提高,从而地区劳动力数量增加,并引致住宅价格上升。此后,住宅价格上升对工业部门的劳动力经过挤出、吸引的反复循环后,促进工业部门转移,工业份额下降;而对于服务业部门,住宅价格对其经过挤出再吸引的反复循环后,促进服务业扩张。从长期看,“产城融合”使地区服务业占比上升,产业结构升级。
工业、服务业的“互促力”和住宅价格对产业的“挤出力”是一对相反的力量,当“互促力”大于“挤出力”时,住宅价格上升,产业结构升级,而工业的繁荣程度依然上升;当“互促力”小于“挤出力”时,就会发生工业转移。一种极端情况是工业全部转出,由于服务业既是产业的组成部分又是城市功能的供给载体,“产城融合”能够继续在服务业内部螺旋上升。因此,“产城融合”是一种可持续的具有辐射带动作用的发展理念。
五、实证检验与启示(一)实证模型
针对结论a和c,我们设定了实证模型A和B;针对结论b和d,设定了实证模型C和D。模型A、B和C考察短期,模型D考察长期。其中,MPros和SPros分别表示工业和服务业的繁荣程度,RS为表示产业结构,RHP表示住宅价格水平,R表示工资水平,X为控制变量。
| $\begin{gathered} \ln MPro{s_{it}} = \alpha + {\beta _1}\ln MPro{s_{it - 1}} + {\beta _2}\ln SPro{s_{it}} + \hfill \\ {\beta _3}\ln RH{P_{it}} + {\beta _4}\ln R{W_{it}} + {X_{it}} + {\varepsilon _{it}} \hfill \\ \end{gathered} $ | (A) |
| $\begin{gathered} \ln MPro{s_{it}} = \alpha + {\beta _1}\ln SPro{s_{it - 1}} + {\beta _2}\ln MPro{s_{it}} + \hfill \\ {\beta _3}\ln RH{P_{it}} + {\beta _4}\ln R{W_{it}} + {X_{it}} + {\varepsilon _{it}} \hfill \\ \end{gathered} $ | (B) |
| $\ln R{S_{it}} = \alpha + {\beta _1}\ln R{S_{it - 1}} + {\beta _2}\ln RH{P_{it}} + {\beta _3}\ln R{W_{it}} + {X_{it}} + {\varepsilon _{it}}$ | (C) |
| $\ln SPro{s_{it}} = \alpha + {\beta _1}\ln SPro{s_{it - 1}} + {\beta _2}\ln RH{P_{it - 2}} + {\beta _3}\ln R{W_{it}} + {X_{it}} + {\varepsilon _{it}}$ | (D) |
1.样本选择。考虑到“新型城镇化”的背景,本文将样本范围选定在“县域”。由于很难获得全国县域层面的数据,本文以统计资料较为完善且省内经济发展与全国存在相似梯度、速度略快于全国(谢呈阳等,2014)的江苏省县域数据为样本进行实证分析,以保证结果的可参考性。
2.度量指标和数据说明。本文采用县域工业相对产值(RM)和服务业相对产值(RS)来衡量工业繁荣程度和城市功能完备程度,用相对房价(RH)来衡量住宅价格水平,用服务业相对占比(RSR)来衡量产业结构,用相对工资(RW)来衡量工资水平。其中,工业产值与服务业产值直接在年鉴中获得,住宅价格通过县级市房地产开发投资额除以房地产销售面积得到,工资水平指在岗职工平均工资,服务业占比用服务业产值占地区GDP比重来测度。以工业相对产值(RM)为例来说明相对量的计算方法:假设某市的工业产值为mpi,其他所有样本城市的均值为mp,则该市的相对工业产值为mpi/mp。
控制变量包括贸易自由度、教育条件、医疗条件、外贸依存度、与上海的距离以及是否为市辖区。贸易自由度用地区年度货运总量来表示,取对数后记为lnTrade;医疗条件用每年医院、卫生院床位数来表示,取对数后记为lnHealth;与上海的距离通过Google Earth测得,取对数后记为lnDistance;教育条件用中等及以上学校在校生人数占地区人口比重(Edu)来表示;外贸依存度用地区进出口贸易额与同期地区GDP比值(FTD)来表示;市辖区为虚拟变量,记为Urban,取值为0或1。
本文所用数据来自2005-2014年的《江苏统计年鉴》及江苏省13个地级市统计年鉴。在样本期间内,个别行政区发生了撤县划区的变动,本文以2004年为基准,将变动后的区对应于原县级市纳入统计。样本包含65个县级市10年的数据。
(三)实证检验结果本文采用系统广义矩(GMM)方法进行估计,以消除模型存在的内生性和自相关问题。根据GMM方法的适用条件,首先需要进行AR(1)、AR(2)和Sargan检验。AR(1)和AR(2)检验的原假设分别是差分方程的残差序列不存在一阶和二阶序列相关,相应统计量的p值大于0.05时在5%的显著性水平上接受原假设,否则拒绝。由于方程中包含被解释变量的滞后项,AR(1)检验必然拒绝原假设,因此主要考虑AR(2)的检验结果。Sargan检验的原假设是模型估计所选用的所有工具变量都是外生的,相应统计量的p值大于0.05时在5%的显著性水平上接受原假设,否则拒绝。在数据通过Sargan检验和AR(2)检验的前提下,系统GMM估计结果是一致有效的。
1.城市功能完备程度和住宅价格对工业繁荣程度的影响。针对模型A,我们以地区工业相对产值RM作为被解释变量,其滞后一期值L1.RM、服务业相对产值RS、相对住宅价格RH、相对工资RW以及相关控制变量为解释变量,采用系统GMM方法进行估计,并进行Sargan检验和ArellanoBond检验,结果见表1。从中可见,当期城市功能完备程度对工业繁荣程度的影响显著为正,符合结论a的预测;同时,住宅价格对工业繁荣程度的影响显著为负,说明短期住宅价格上升对工业会产生一定的挤出效应,验证了结论b和d的理论预测。
| 模型 A | 模型B | ||
| L1.RS | 0.9069 ***(0.0008) | ||
| L1.RM | 0.0460 ***(0.0021) | ||
| RS | 0.7362 ***(0.0046) | ||
| RM | 0.0795 ***(0.0006) | ||
| RH | -0.0450 ** (0.0522) | -0.0133 ***(0.0013) | |
| RW | 0.7220 ***(0 .0126) | -0.0085 *** (0.0038) | |
| ln Trade | 0.1913 ***(0.0056) | -0.0590 ***(0.0023) | |
| ln Health | -0.7332 *** (0.0129) | 0.2061 ***(0.0040) | |
| Edu | 0.1795 ***(0.0117) | 0.0661 ***(0.0036) | |
| ln Distance | 0.2890 ***(0.0150) | -0.0036(0.0041) | |
| FTD | 1.1948 ***(0.0075) | 0.0343 ***(0.0026) | |
| Urban | 0.1609 ***(0.0215) | -0.2232 ***(0.0032) | |
| Cons | 2.0462 ***(0.1121) | -1.1253 ***(0.0233) | |
| Sargan检验P值 | 0.1399 | 0.0863 | |
| AR(1)检验P值 | 0.0122 | 0.0372 | |
| AR(2)检验P值 | 0.3207 | 0.1249 | |
| 注:括号内为标准差, ***、 **和 *分别表示在1%、5%和10%的水平上显著,下表同。 | |||
2.工业繁荣程度和房价水平对城市功能完备程度(服务业繁荣程度)的影响。针对模型B,我们以地区服务业相对产值RS为被解释变量,其滞后一期值L1.RS、工业相对产值RM、相对住宅价格RH、相对工资RW以及相关控制变量为解释变量,估计和检验结果见表1。模型中工业繁荣程度对城市功能完备程度的影响显著为正,与结论c相符。同时,当期住宅价格对当期城市功能完备程度(服务业繁荣程度)存在显著的负向影响,住宅价格上升对服务业的挤出系数为0.013,小于模型A中其对工业的挤出系数0.045,从而证明了理论分析中“房价上升对工业的挤出效应大于服务业”的结论。
3.住宅价格对城镇产业结构的影响。针对模型C,我们以地区服务业相对比重RSR为被解释变量,其滞后一期值L1.RSR、相对房价RH、相对工资RW以及相关控制变量作为解释变量;针对模型D,以地区服务业相对产值RS为被解释变量,以其滞后一期值L1.RS、相对房价RH的滞后两期值L2.RH、相对工资RW以及相关控制变量为解释变量,估计和检验结果见表2。
| 模型 C | 模型D | |
| L1.RSR | 0.8924 ***(0.0254) | |
| L1.RS | 0.9429 ***(0.0008) | |
| RH | 0.0116 ***(0.0027) | |
| L2.RH | 0.0303 ***(0.0019) | |
| RW | 0.0560 ***(0.0059) | -0.0697 ***(0.0028) |
| ln Trade | -0.0043 **(0.0021) | -0.0711 ***(0.0013) |
| ln Health | 0.0717 ***(0.0040) | 0.1200 ***(0.0033) |
| Edu | 0.0143 ***(0.0040) | -0.0481 ***(0.0037) |
| ln Distance | 0.0338 ***(0.0061) | -0.1312 ***(0.0043) |
| FTD | 0.0328 ***(0.0047) | 0.0169 ***(0.0031) |
| Urban | -0.0704 ***(0.0059) | -0.1208 ***(0.0048) |
| Cons | -0.6667 ***(0 .0349) | 0.3557 ***(0.0389) |
| Sargan检验P值 | 0.1058 | 0.0612 |
| AR(1)检验P值 | 0.0001 | 0.0239 |
| AR(2)检验P值 | 0.3185 | 0.1848 |
表2中检验结果表明,在短期内,住宅价格与服务业比重显著正相关,房价每上升1个单位,服务业比重上升0.012个单位;从长期看,住宅价格与城市功能完备程度显著正相关,住宅价格每上升1个单位,两年后城市功能完备程度上升0.030个单位。至此,本文证明了结论b和d,即“产城融合”能够通过住宅价格调节城镇产业结构,促进产业结构升级,在长期促进产业繁荣。
(四)启示第一,在中国大多数县域,相对于空间规模,城镇的产业基础有待进一步加强。模型A中城市功能完备程度对工业繁荣程度的拉升系数为0.736,远大于产业发展引致的住宅价格上升对工业的挤出系数0.045;同时,模型B中工业对服务业的拉升系数为0.080,亦大于产业发展引致的住宅价格上升对服务业的挤出系数0.013。这表明在本文研究的空间和时间内,产业发展所需的城镇空间较富足。由于江苏省在中国属于经济先发地区,可以推断中国大多数县域的产业基础都有较大的加强空间。
城镇发展中的产业基础不足与在过去一段时间内过于追求“城镇化率”、盲目开展“造城”运动,而忽视城市空间、产业基础和劳动力效用三者之间应有的匹配程度有关。因此,未来在城镇化的推进过程中,需审慎评估城镇建设的规模,适当控制“城镇”地域空间的盲目扩张,强化已有城镇空间的产业发展,提高“产”、“人”、“城”的融合程度。
第二,相对于工业的发展程度,中国大多数县域的城市功能完备程度有待提高。根据模型A和模型B的结果,城市功能完备程度对工业繁荣程度的拉动系数(0.736)远大于工业对城市功能完备程度的拉动系数(0.080),城市功能完备程度的拉动系数(0.907)也远大于工业对其的拉动系数(0.080)。依据边际递减原理,大多数县域的城市功能完备程度远落后于工业发展速度。这一问题与长期以来中国的城镇化是以工业化为手段推动的有关。在很多的工业镇或者是“生产外置型”城区,服务业严重缺失,无法吸引产业发展所需的高端人才。这也是中国很多地方单纯以工业化带动城镇化无法推进的原因。
由于当前完善城市功能的外部性更大,中国在新型城镇化建设中要尽快摆脱“先生产,后生活”的传统观念,由“各类要素围绕工业配套”转向“各类要素围绕人的需求配套”。有条件的地区甚至可以适当突破第一、第二、第三产业发展的常规路径,有目的地引导和推动服务业适度超前发展,从而实现产业与城市长期协同发展。具体而言,在制定城镇发展规划时要充分考虑未来发展对城市功能的需求和已有服务业的服务半径,同步甚至超前发展城市生活配套设施,将商业综合体的建设纳入发展规划,通过探索建立政府投资、价格协同等合理回报机制,确保服务业项目一开始就能与工业项目一样获得稳定的多元化的投资。
六、结论与研究展望在新型城镇化“以人为本”的大背景下,作为其主导理念之一的“产城融合”应该是“产业”、“人”和“城市功能”三者的融合。以“人”的效用为出发点构建的理论模型所论证的“产城融合”发展理念对城镇建设的推动作用具有一般性。
“产”与“城”之间能够协同互促,其根本机理在于:第一,连接两者的“人”既是产业发展的重要投入要素,又对城市功能存在必然需求;第二,作为“产”组成部分的服务业是城市功能的实现载体。因此,一方面,产业的繁荣会对城市功能产生引致需求,促进城市功能的完备;另一方面,完备的城市功能又能吸引更多的“人”服务于产业发展。“产”、“城”之间的协同作用是通过产品及要素市场的价格调节和因果循环机制实现的。
本文以江苏省县域数据为样本的实证分析结果验证了理论模型的结论。同时,本文结果还表明,目前中国大多县域的“产城融合”并未得到很好的推进,主要体现在:第一,相对于城镇的空间规模,产业基础尚显薄弱;第二,相对于城镇的工业发展水平,城市功能配套尚欠缺。以上两个问题起因于城镇化过程中盲目“造城”运动和工业化的单一拉动手段,可能带来地区产业空心化、地区发展“人才瓶颈”等一系列非可持续发展问题。因此,在推进新型城镇化方面需要做到:第一,适当控制“城镇”空间的盲目扩张,强化已有城镇空间的产业基础;第二,围绕“人”的需求,重视服务业配套,以实现产业与城镇的长期协同发展。此外,由于现阶段完善城市功能的正外部性较大,有条件的地区可以适当突破第一、第二、第三产业发展的常规路径,有目的地引导和推动服务业适度超前发展。
诚然,在中国新型城镇化的推进过程中,产业与城市(镇)的协同发展问题远非“融合”二字所能概括。基于本文的研究,至少还有3个问题值得进一步探索:怎样的产业结构和空间布局才能更好地服务于城镇化过程中“人”的需求?如何在产业结构重构的过程中更好地引导产业转移以辐射城镇周边?如何在要素结构存在差异的不同城镇因地制宜地推进“产城融合”战略?
| [1] | 范剑勇,邵挺.房价水平、差异化产品区位分布与城市体系[J].经济研究,2011,(2):87-99. |
| [2] | 蒋华东.产城融合发展及其城市建设的互融性探讨——以四川省天府新区为例[J].经济体制改革,2012,(6):43-47. |
| [3] | 江小涓.服务业增长:真实含义、多重影响和发展趋势[J].经济研究,2011,(4):4-14. |
| [4] | 孔翔,杨帆."产城融合"发展与开发区的转型升级——基于对江苏昆山的实地调研[J].经济问题探索,2013,(5):124-128. |
| [5] | 谢呈阳,周海波,胡汉辉.产业转移中要素资源的空间错配和经济效率损失[J].中国工业经济,2014,(12):130-142. |
| [6] | 杨立勋,姜增明.产业结构与城镇化匹配协调及其效率分析[J].经济问题探索,2013,(10):34-39. |
| [7] | Browning H,Singelman J.The emergence of a service society:Demographic and sociological aspect of the sectorial transformation of the labor force[A].Springfield V A.National technical information service[C].VA:USA Springfield,1975. |
| [8] | Helpman E.The size of regions[A].Pines D,Sadka E,Zilcha I.Topics in public economics[C].Cambridge:Cambridge University Press,1998. |
| [9] | Hill T P.On goods and services[J].Review of Income and Wealth,1977,23(4):315-338. |
| [10] | Krugman P.Increasing returns and economic geography[J].Journal of Political Economy,1991,99(3):483-499. |
 2016, Vol. 42
2016, Vol. 42


