文章信息
 | 财经研究 2017年43卷第12期 |
- 杜在超, Juan Carlos Escanciano,
- Du Zaichao, Juan Carlos Escanciano.
- 期望损失的后验分析
- Backtesting expected shortfall:accounting for tail risk
- 财经研究, 2017, 43(12): 74-99
- Journal of Finance and Economics, 2017, 43(12): 74-99.
-
文章历史
- 收稿日期:2017-06-28

2017第43卷第12期
编者按
量化市场风险对于期权定价、投资、金融监管和风险管理具有重要意义。而风险量化的关键在于选择科学的评估指标和工具。本期《财经研究》“海外归来”栏目翻译了西南财经大学经济与管理研究院杜在超教授和美国印第安纳大学Juan Carlos Escanciano教授在Management Science 2017年第4期合作发表的论文“Backtesting Expected Shortfall:Accounting for tail risk”。①该文首次提出了期望损失模型的后验分析方法,填补了金融风险管理领域的一个空白,也可为国内金融机构和学者提供借鉴和参考。
① 原文版权归属INFORMS(http://www.informs.org),译文已获得原文的中文翻译版权。中文译文中出现的错误INFORMS概不负责,中文译文文责作者自负。我们感谢张栋浩在中文译稿中的大力帮助。Management Science是管理类国际顶级期刊。杜在超教授于2010年获得印第安纳大学经济学博士学位,2010年8月回国任教,2015年被评为教育部首届青年长江学者,主要研究领域包括金融计量和应用计量。
2. 美国印第安纳大学文理学院经济系,布鲁明顿 47405
2. Department of Economics, Indiana University, Bloomington IN 47405, USA
一、引言
市场风险的量化是学者和金融机构普遍感兴趣的问题,这对于期权定价、投资组合以及风险管理都非常重要。20世纪90年代以来,度量市场风险的主要指标是在险价值(VaR,Value-at-Risk)(Jorion,2006;Christoffersen,2009)。VaR描述了在给定置信水平的情况下,一个投资组合可能遭受的最大损失。尽管VaR概念简单、计算方便,但是它却不是一个很好的风险度量指标。VaR没有考虑尾部风险,它仅仅告诉我们在没有发生尾部事件时的最大损失,但没有指出尾部事件发生时可能遭受的损失大小。VaR也存在其他的缺陷,包括不满足次可加性(Artzner等,1997,1999;Acerbi和Tasche,2002)和凸性(Basak和Shapiro,2001)。期望损失(ES,Expected Shortfall)克服了上述VaR的缺陷,是一种满足“一致性”的风险度量指标,ES计算了超过给定置信水平的损失的平均值①。在2012年5月3日的巴塞尔协议III中,巴塞尔委员会明确地提出要逐步淘汰VaR,并采用ES作为替代指标。但是,使用ES作为度量市场风险的主要指标面临的一大挑战是,没有工具对ES进行评估(Yamai和Yoshiba,2002,2005;Kerkhof和Melenberg,2004)。本文的主要目的就是提供这样的评估工具。
① ES其他名称包括:条件VaR、平均VaR、尾部VaR或者平均尾部损失。
我们提出的方法主要是基于下面的观察。对每个置信水平而言,如果VaR模型是设定正确的,中心化的碰撞序列(投资组合损失超过VaR与否)应该是一个鞅差序列(Berkowitz, Christoffersen和Pelletier,2011)。如果在左侧尾部的置信区间内求取中心化碰撞序的积分,也可以形成一个鞅差序列,我们把它叫做“累积碰撞序列”。就像ES是左侧尾部VaR的积分一样,累积碰撞序列是对左侧尾部所有碰撞序列的积分。因此,我们可以通过检验累积碰撞序列是否为鞅差序列来检验ES模型(Escanciano和Lobato,2009a)。具体而言,我们提出了一种Box-Pierce形式的检验(Box和Pierce,1970)。我们的Box-Pierce检验是对以往文献关于VaR条件后验分析的自然推广(Christoffersen,1998;Berkowitz, Christoffersen和Pelletier,2011)。同样地,我们基于累积碰撞序列的t检验是对VaR无条件后验分析的自然推广(Kupiec,1995)。McNeil和Frey(2000)、Berkowitz(2001)、Kerkhof和Melenberg(2004)、Wong(2008,2010)以及Acerbi和Szekely(2014)曾提出了ES的无条件后验分析方法,而本文是第一个提出ES条件后验分析方法的文章②。但是出于完整性考虑,我们也报告了无条件后验分析的结果。
② 众所周知,对常用的模型(比如说,滤波历史模拟法)而言,条件后验分析比无条件后验分析更有检验力(Escanciano和Pei,2012)。
我们对ES的后验分析考虑了有碍参数估计对检验的影响。已有文献对VaR或ES预测的估计误差进行了广泛研究,包括Christoffersen和Goncalves(2005)、Gourieroux和Zakoian(2013)以及Francq和Zakoian(2015)。Escanciano和Olmo(2010)研究了VaR后验分析存在的估计风险。针对ES后验分析的文献,只有Kerkhof和Melenberg(2004)在对无条件后验分析进行历史模拟时考虑了估计风险。与Escanciano和Olmo(2010)类似,我们从理论和模拟上证明了,当样本内观测没有比样本外观测大很多的时候,忽略估计风险将会给ES后验分析带来极大的Size扭曲(size distortions)。为了解决该局限性,我们提出了修正的后验分析,该方法充分考虑了估计风险,并通过蒙特卡洛模拟证明了稳健性。
本文想传达的主要信息是,与大多数学术和非学术文献相反,ES后验分析并没有比VaR后验分析困难很多③。我们提出的后验分析很容易执行,是对VaR后验分析方法的自然推广,也可以作为巴塞尔委员会建议的内部模型方法的工具箱,因此可谓是一个可以更好捕捉尾部事件的市场风险度量与评估。
③ 我们的观点与Kerkhof and Melenberg(2005)、Acerbi和Szekely(2014)相同。并且,Acerbi和Szekely(2014)讨论了对ES做后验分析的可能性,以及阐述了“诱发性”(Elicitability)的概念。
本文余下内容安排如下。第二部分介绍本文常用的表达符号,以及后验分析所涉及的基本内容。第三部分我们提出新的无条件和条件后验分析,并求解它们的渐进性质。第四部分通过蒙特卡洛模拟研究后验分析的有限样本表现。第五部分采用金融危机后的日度数据,将本文提出的后验分析应用于三大主要股票指数,包括标普500、德国DAX指数以及恒生指数。实证结果显示,VaR对金融危机期间的极端事件的反应较为迟钝,而ES则提供了尾部风险的准确描述。第六部分总结全文。附录是本文的数学证明。
二、累积碰撞序列
Yt是银行在t时刻的收益,Ωt-1是风险管理者获得的t-1期的信息集,包括Yt的滞后值以及其他变量Xt的滞后值。也就是,Ωt-1={Xt-1, Xt-2, …; Yt-1, Yt-2, …}。我们假设,{ Yt, Xt} t=∞∞是严格平稳、遍历性过程,参考Escanciano(2007)的研究,我们的结果也可以扩展到一些非严格平稳和非遍历性序列中。G(., Ωt-1)是给定Ωt-1时Yt的条件累积分布函数,即G(., Ωt-1)=Pr(Yt≤.|Ωt-1)。为了表达的简便,我们在所有包含随机变量的等式中删去了“almost surely”的说法。假设G(., Ωt-1)是连续的。将α∈[0, 1]记为置信水平。α置信水平的VaR定义如下:
| $ \Pr \left( {{Y_t} \le - Va{R_t}\left( \alpha \right)\left| {{\mathit{\Omega }_{t - 1}}} \right.} \right) = \alpha $ | (1) |
也就是说,-VaRt(α)是累积分布函数G在α分位点的取值,VaRt(α)=-G-1(α, Ωt-1)=-inf{y:G(y, Ωt-1)≥α}。
定义时刻t,置信水平α时的碰撞序列是ht(α)=1(Yt≤VaRt(α)),其中,1(.)是示性函数。当t时刻的损失大于等于VaRt(α)时,示性函数取值1,否则取值0。(1)式的含义是碰撞序列是一个均值为α的伯努利变量,并且对于每一个α∈[0, 1],中心化的碰撞序列(centered violations)都是鞅差序列,即对每一个α∈[0, 1],都有E[ht(α)-α|Ωt-1]=0。
这个约束条件已经成为对VaR进行后验分析的基础。它的两个主要推论包括碰撞序列{ ht(α)-α} t=1∞的零均值性质和不相关性质,分别是Kupiec(1995)的无条件后验分析以及Chirstoffersen(1998)的条件后验分析的基础。这也是最为广泛使用的后验分析方法。
VaR由于没有捕捉尾部风险而被广泛批评。这也可以从碰撞序列{ ht(α)-α} t=1∞中看出来,它仅仅包含了损失是否超过VaR的信息,但是并没有包含尾部事件所造成的损失额信息。VaR没有捕捉尾部风险的缺陷加上其他方面的不足,促使了ES概念的形成。ES在度量投资组合风险时,既考虑了损失超过一定置信水平的可能性,也考虑了损失的规模大小。ES的定义是超过VaRt(α)的条件期望损失,也就是:
| $ E{S_t}\left( \alpha \right) = E\left[ { - {Y_t}\left| {{\mathit{\Omega }_{t - 1}}} \right., - Y > Va{R_t}\left( \alpha \right)} \right] $ | (2) |
通过条件概率以及变量转换,可以将ESt(α)表达为VaRt(α)的一个函数:
| $ E{S_t}\left( \alpha \right) = \frac{1}{\alpha }\int_o^\alpha {Va{R_t}\left( u \right)du} $ | (3) |
不像VaRt(α)只包含了α分位点的信息,ESt(α)通过对VaRs从0到α积分,包含了整个左侧尾部的信息。为了检验ESt(α)是否设定正确,很自然想到要对ht(α)进行积分,也就是累积碰撞序列Ht(α)
因为ht(u)的均值是u,通过Fubini定理可得,Ht(α)的均值是1/α
为了计算方便,定义ut=G(Yt, Ωt-1)。采用ht(u)=1(Yt≤-VaRt(u))=1(ut≤u),我们可以得到:
| $ {H_t}\left( \alpha \right) = \frac{1}{\alpha }\int_o^\alpha {1\left( {{u_t} \le u} \right)du} = \frac{1}{\alpha }\left( {\alpha - {u_t}} \right)1\left( {{u_t} \le a} \right) $ | (4) |
与碰撞序列相似,累积碰撞序列与Yt的分布无关,因为{ ut} t=1∞包括了服从独立同均匀分布的变量(Rosenblatt,1952;Berkowitz,2001;Hong和Li,2005)。Acerbi和Tasche(2002)以及Emmer等(2014)采用4个式子的黎曼和(Riemann sum)对(3)式的积分进行了近似估计。①累积碰撞序列可以不采用近似求解方法,因为(4)式的积分可以直接计算出来。但是与碰撞序列不同,累积碰撞序列还包括了尾部风险:当碰撞序列等于零时,累积碰撞序列也是零;当碰撞序列不等于零时,累积碰撞序列通过α-ut计算了Yt的实际值与置信水平之间的差距。其中,α-ut=G(G-1(α, Ω-1), Ω-1)-G(Yt, Ω-1)。②
① 同样可以参考在一个风险水平的子集上对VaR做后验分析的文献,包括Hurlin和Tokpavi(2006)、Perignon和Smith(2008)以及Colletaz等(2013)。
② 实际上,d(y, x)=|G(y, Ω-1)-G(x, Ω-1)|是一个距离函数。
由于分布函数G是未知的,所以构造{Ht(α)} t=1∞的变量{ut} t=1∞也是未知的。在实践中,学者和风险管理人员可以通过设定参数条件分布函数G(., Ωt-1, θ0)以及估计未知参数θ0的办法,来计算VaR或ES。一般来说,选择服从Student-t分布的位置尺度模型(Location-Scale Models)来刻画分布函数G(., Ωt-1, θ0)。在我们的模型设定中,当然也可以考虑其他的模型选择。③在选定了参数模型之后,可以定义“广义误差”,ut(θ0)=G(Yt, Ωt-1, θ0),以及与之相关的累积碰撞序列Ht(α)=
③ 我们可以将该方法扩展到半参数设定中,其中θ0包括一个无穷维的元素。我们将在以后的研究中对此问题进行扩展。
上述论据为ES的后验分析提供了理论基础。我们可以通过检验{Ht(α, θ0)-α/2} t=1∞是否具有零均值,对ES做无条件后验分析;通过检验{Ht(α, θ0)-α/2} t=1∞是否序列相关,对ES做条件后验分析。在下一节,我们将提出这些假设的检验统计量。
三、ES后验分析
在本节,我们提出ES的后验分析方法。ES的无条件后验分析是一个简单的t检验,原假设是E[Ht(α, θ0)]=α/2,该检验是Kupiec(1995)提出的VaR无条件后验分析的推广。ES条件后验分析是一个Box-Pierce检验,这也是Christoffersen(1998)和Berkowitz等(2011)提出的VaR条件后验分析的自然推广。我们首先研究了一般后验分析方法(考虑了估计风险)的渐进分布,并且证明了不考虑估计风险可能会导致极大的size扭曲。继而,我们又提出了对估计风险稳健的修正后验分析方法。
(一) 一般无条件和条件后验分析
在实践中,模型的参数θ0是未知的,为了构造ES的预测而需要估计θ0。为了行文的简单,我们采用固定预测机制,但是本文理论可以一般化地推广到其他预测机制上(比如,移动窗口和递归机制);对此问题,可以参考Escanciano和Olmo(2010)及其他相关文献。具体而言,样本内共T期{Y-T+1, Ω-T, …, Y0, Ω-1}用来估计参数θ0,即
然后,采用时间长度为n的样本外观测{Y1, Ω0, …, Yn, Ωn-1}来评估ES模型(后验分析)。我们的后验分析是基于累积碰撞序列的估计值。
ES的无条件后验分析是一个标准的t检验,原假设是H0u: E(Ht(α, θ0))=α/2。
经过简单计算可知,E(Ht2(α))=α/3,以及Var(Ht(α))=α(1/3-α/4)。因此,一个简单的t检验统计量是UES=
由于参数估计效应(estimation effect)的存在,UES的渐进分布一般不服从标准正态,而是依赖于样本内时间T和样本外时间n的渐进相对大小。假设,T和n都趋近于无穷大,并且n/T→λ<∞。定理1给出了UES的极限分布,其中Ft(θ, x)是参数误差ut(θ)的条件累积分布函数,Ft(θ, x)≡Pr[ut(θ)≤x|Ωt-1],lt是估计值
定理 1 在附录A中的假设A0-A4下,UES→dN(0, σλ2(α)),其中,
| $ \sigma _\lambda ^2\left( \alpha \right) = \frac{{\alpha \left( {1/3 - \alpha /4} \right) + \lambda {{R'}_{ES}}E\left[ {{l_t}{{l'}_t}} \right]{R_{ES}}}}{{\alpha \left( {1/3 - \alpha /4} \right)}}, $ |
这里RES=1/α·E[
注释 1:类似于Escanciano和Olmo(2010),我们在定理1的证明中量化了参数估计效应,具体为:
| $ \sqrt n \left( {\bar H\left( \alpha \right) - \frac{\alpha }{2}} \right) = \frac{1}{{\sqrt n }}\sum\limits_{t = 1}^n {\left[ {{H_t}\left( {\alpha ,{\theta _0}} \right) - \frac{\alpha }{2}} \right]} + \underbrace {\frac{{\sqrt \lambda }}{{\sqrt n }}{{R'}_{ES}}\sum\limits_{t = - T + 1}^0 {{l_t} + op\left( 1 \right)} }_{Estimation\;Effect}, $ |
附录B中给出了RES的详细表达式,包括在一般的位置尺度模型中的具体表达式。λ=0是定理1的特殊情况,即样本内观测显著大于样本外观测。当λ=0时,UES服从标准正态的极限分布,无条件后验分析的推论将会极大简化。
推论 1 在定理1的假设下以及λ=0,UES→dN(0, 1)。
接下来,我们讨论ES的条件后验分析。原假设是H0c:E[Ht(α, θo),α/2|Ωt-1]=0,该原假设是对VaR条件后验分析原假设的自然推广(Christoffersen,1998)。我们需要如下的符号。定义Ht(α)滞后j阶(j≥0)的自协方差和自相关系数是rj=Cov(Ht(α),Ht-j(α))和ρj=
在自相关系数的定义中,我们代进了均值等于α/2的约束,这使得基于γnj的检验对原假设Hoc具有更强的检验效能(power)。①但是,在我们目前的设定中,{ Ht(α) }t=1∞不可观测、θ0未知、Ωt-1也不可完全观测,所以我们需要将Ht(α)替换为
① 经过一些代数计算可得,γnj近似等于
| $ {{\hat r}_{nj}} = \frac{1}{{n - j}}\sum\limits_{t = 1 + j}^n {\left( {{{\hat H}_t}\left( \alpha \right) - \alpha /2} \right)\left( {{{\hat H}_{t - j}}\left( \alpha \right) - \alpha /2} \right)} \;和\;{{\hat \rho }_{nj}} = \frac{{{{\hat r}_{nj}}}}{{{{\hat r}_{n0}}}}。$ |
注意在原假设Hoc下,对于j≥1都有ρj=0。所以,可以通过
| $ {C_{ES}}\left( m \right) = n\sum\limits_{j = 1}^m {\hat \rho _{nj}^2} $ | (6) |
至于无条件后验分析,CES(m)的渐进分布不仅依赖于λ,还依赖于其他的未知量。
定理 2 在附录A的假设A0-A4下,CES(m)→d
| $ \sum\nolimits_{ij} { = {\delta _{ij}}} + \lambda {{R'}_i}E\left( {{l_t}{{l'}_t}} \right){R_j} $ | (7) |
| $ {R_j} = \frac{1}{{\alpha \left( {1/3 - \alpha /4} \right)}}E\left[ {\left( {{H_{t - j}}\left( \alpha \right) - \alpha /2} \right)\int_0^\alpha {\frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }}dx} } \right] $ | (8) |
δij是克罗内克函数(Kronecker delta function),该函数在i=j时取值1,否则取值0。{Zj}是服从独立标准正态分布的变量。
从定理2可知,CES(m)服从一个加权的卡方极限分布。该权重是Rj的函数,因为与Yt的分布有关。但当λ=0时,也就是πj=1(对于任意的j=1, …, m),CES(m)就服从标准极限分布。
推论 2 在定理2的假设下以及λ=0,CES(m)→dχm2,其中,χm2是自由度为m的卡方分布。
综上可知,当λ=0时,本文提出的无条件和条件后验分析在零假设下具有标准极限分布;但当λ>0时,它们不再具有标准极限分布。这说明,除非T显著大于n(比如T=2500,n=250),否则基于标准分布临界值的基本检验不能控制第一类错误(Type-Ierror)。为了避免发生该问题,我们提出对估计风险稳健的修正后验分析。
(二) 修正的无条件和条件后验分析
在本节,我们提出修正的后验分析方法,该方法明确考虑了估计效应(estimation effect),并且对于任意的λ(0≤λ<∞)都有标准极限分布。定理1给出了无条件后验分析(式5)的估计效应表达式,据此我们提出如下的修正检验统计量:
| $ M{U_{ES}} = \frac{{\sqrt n \left( {\bar H\left( \alpha \right) - \alpha /2} \right)}}{{\sqrt {\alpha \left( {1/3 - \alpha /4} \right) + \frac{n}{T}{{R'}_{ES}}{W_T}{R_{ES}}} }} $ |
其中,
类似地,通过定理2可以按照下式修正原有的条件后验分析(式子6),MCES(m)=
在附录B中,我们给出了位置尺度模型的
从定理1和定理2可知,无论λ取何值,修正的检验统计量MUES和MCES(m)都服从标准极限分布。
推论 3 在定理1的假设下以及
推论 4 在定理2的假设下以及
如推论1和推论2所示,一般检验统计量只在λ=0时具有标准极限分布;而推论3和推论4表明,稳健的检验统计量对任意的0≤λ<∞都具有标准极限分布。
四、蒙特卡洛模拟
我们采用蒙特卡洛模拟评估本文后验分析方法的有限样本表现。为了便于比较,我们同时汇报了ES和VaR的检验结果。参照Kerkhof和Melenberg(2004)及其他相关文献,我们为ES选择了比VaR更大的置信水平α。具体而言,根据经验准则,我们为ES选择了比VaR大两倍(或接近于两倍)的置信水平,从而使碰撞序列和累积碰撞序列的期望值保持一致(或接近一致)。在模拟中,我们为ES设定的置信水平包括α=0.1,0.05以及0.025,对应的VaR置信水平是α=0.05,0.025以及0.01。我们比较ES和VaR的无条件后验分析和条件后验分析。其中,VaR的后验分析是UVaR=
我们采用常用的AR(1)-GARCH(1, 1)设定Yt的真模型(原假设),此时VaR和ES的表达式是:
| $ \begin{array}{l} Va{R_t}\left( \alpha \right) = - {a_0}{Y_{t - 1}} - {\sigma _t}F_v^{ - 1}\left( \alpha \right),\sigma _t^2 = {\omega _0} + {\alpha _0}{Y_{t - 1}} + {\beta _0}\sigma _{t - 1}^2\\ E{S_t}\left( \alpha \right) = - {a_0}{Y_{t - 1}} - {\sigma _t}m\left( \alpha \right),m\left( \alpha \right) = E\left[ {{\varepsilon _t}\left| {{\varepsilon _t} \le F_v^{ - 1}\left( \alpha \right)} \right.} \right] \end{array} $ | (9) |
其中,εt服从自由度是v(未知)的Student-t分布,即εt~tv,其中α分位数记为Fv-1(α)。我们将参数θ0的真实值设定为θ0=(a0, ω0, α0, β0)=(0.05, 0.05, 0.1, 0.85)以及v=5,这也是实证文献中典型的参数值。
在每次模拟中,我们都采用CMLE方法估计θ0和v,从而得到
① 关于m=1和3的模拟结果,读者如有兴趣,可以向作者索取。
Yt数据生成过程的原假设和备择假设如下,
H0:AR(1)-GARCH(1,1)模型,
| $ \begin{array}{l} {Y_t} = 0.05{Y_{t - 1}} + {v_t},{v_t} = {\sigma _t}{\varepsilon _t},{\varepsilon _t} \sim {t_5}\\ \sigma _t^2 = 0.05 + 0.1Y_{t - 1}^2 + 0.85 + \sigma _{t - 1}^2 \end{array} $ | (10) |
A1:TAR模型,Yt=atYt-1+vt, vt=σtεt
| $ \begin{array}{l} \sigma _t^2 = 0.04 + 0.1v_{t - 1}^2 + 0.89\sigma _{t - 1}^2\\ {a_t} = 0.7 \times 1\left( {{v_{t - 1}} \le - 2} \right)。\end{array} $ |
A2:均值GARCH模型,Yt=2.5σt2+vt, vt=σtεt
| $ \sigma _t^2 = 0.01 + 0.29v_{t - 1}^2 + 0.7\sigma _{t - 1}^2。$ |
A3:AR(1)-ARCH(2)模型,Yt =0.05Yt-1+vt, vt=σtεt
| $ \sigma _t^2 = 0.1 + 0.1v_{t - 1}^2 + 0.8v_{t - 2}^2。$ |
A4:AR(1)-EGARCH(1, 1)模型,Yt=0.05Yt-1+vt, vt=htεt
| $ \ln h_t^2 = 0.01 + 0.9\ln h_{t - 1}^2 + 0.3\left( {\left| {{\varepsilon _{t - 1}}} \right| - \sqrt {2/{\rm{ \mathsf{ π} }}} } \right) - 0.8{\varepsilon _{t - 1}}。$ |
A5:AR(1)-Stochastic Volatility模型,Yt=0.05Yt-1+vt, vt=htεt
| $ \begin{array}{l} h_t^2 = 0.1Y_{t - 1}^2 + \exp \left( {0.98\ln h_{t - 1}^2 + {e_t}} \right)\\ {e_t} \sim iidN\left( {0,1} \right)。\end{array} $ |
A6:AR(1)-GARCH(1, 1)并且具有混合正态残差项,Yt与(10)式相同,
| $ {e_t} \sim \left[ {0.6 \cdot N\left( {1,\sqrt 2 } \right) + 0.4 \cdot N\left( { - 1.5,\sqrt {0.75} } \right)} \right]/\sqrt 3 。$ |
除非被另外设定,在这些模型中{εt}~iid t5。Escanciano和Velasco(2010)、Escanciano和Olmo(2010)采用了类似的模型。A1和A2中的条件均值没有被正确设定,A3、A4和A5中的条件方差没有被正确设定,A6中则是误差项{εt}的分布没有被正确设定。
表 1-9汇报了在5%显著性水平下各检验的实证size和size-corrected powers。①与前文理论一致,当T较小时,估计效应导致基本检验存在严重的size扭曲(犯第一类错误的可能性很高);但当T很大时(比如,T=2 500),size扭曲的程度显著下降。除了VaR的条件后验分析MCVaR(5)存在一些过度拒绝的情形外,修正的后验分析在T很小时仍可以得到满意的size。因为在尾部存在很少的观测值,所以ESt(0.025)和VaRt(0.01)后验分析的size扭曲程度最大。对于给定的样本内观测T,修正的ES后验分析MUES和MCES(5)的size表现,随着样本外观测n从250增加到500而显著改善,这与基本检验的结论相反。
① Size:犯第一类错误的概率,即在原假设为真的情况下,拒绝了原假设;Power:不犯第二类假设的概率,即在原假设为假的情况下,拒绝了原假设。
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.169 | 0.150 | 0.118 | 0.103 | 0.043 | 0.039 | 0.053 | 0.075 |
| A1 | 0.080 | 0.096 | 0.218 | 0.164 | 0.077 | 0.086 | 0.207 | 0.235 |
| A2 | 0.549 | 0.578 | 0.229 | 0.197 | 0.478 | 0.209 | 0.212 | 0.052 |
| A3 | 0.035 | 0.052 | 0.130 | 0.096 | 0.006 | 0.011 | 0.155 | 0.137 |
| A4 | 0.063 | 0.076 | 0.206 | 0.142 | 0.012 | 0.022 | 0.199 | 0.169 |
| A5 | 0.072 | 0.084 | 0.101 | 0.076 | 0.075 | 0.050 | 0.114 | 0.085 |
| A6 | 0.351 | 0.509 | 0.230 | 0.227 | 0.441 | 0.557 | 0.236 | 0.203 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.230 | 0.214 | 0.125 | 0.107 | 0.044 | 0.043 | 0.057 | 0.064 |
| A1 | 0.086 | 0.088 | 0.356 | 0.298 | 0.079 | 0.098 | 0.249 | 0.393 |
| A2 | 0.651 | 0.596 | 0.283 | 0.216 | 0.564 | 0.229 | 0.219 | 0.056 |
| A3 | 0.044 | 0.043 | 0.190 | 0.154 | 0.004 | 0.004 | 0.244 | 0.237 |
| A4 | 0.063 | 0.062 | 0.284 | 0.197 | 0.019 | 0.020 | 0.248 | 0.237 |
| A5 | 0.076 | 0.076 | 0.114 | 0.110 | 0.091 | 0.062 | 0.130 | 0.086 |
| A6 | 0.409 | 0.531 | 0.294 | 0.314 | 0.518 | 0.667 | 0.295 | 0.295 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.176 | 0.114 | 0.140 | 0.155 | 0.051 | 0.042 | 0.073 | 0.120 |
| A1 | 0.052 | 0.043 | 0.131 | 0.117 | 0.071 | 0.082 | 0.089 | 0.102 |
| A2 | 0.358 | 0.193 | 0.180 | 0.048 | 0.418 | 0.138 | 0.151 | 0.022 |
| A3 | 0.041 | 0.029 | 0.094 | 0.081 | 0.014 | 0.008 | 0.081 | 0.080 |
| A4 | 0.048 | 0.037 | 0.123 | 0.115 | 0.013 | 0.012 | 0.104 | 0.101 |
| A5 | 0.038 | 0.024 | 0.055 | 0.055 | 0.069 | 0.064 | 0.059 | 0.035 |
| A6 | 0.673 | 0.314 | 0.492 | 0.066 | 0.776 | 0.786 | 0.483 | 0.045 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.234 | 0.222 | 0.129 | 0.123 | 0.048 | 0.044 | 0.060 | 0.103 |
| A1 | 0.065 | 0.081 | 0.225 | 0.177 | 0.074 | 0.097 | 0.145 | 0.205 |
| A2 | 0.479 | 0.468 | 0.222 | 0.186 | 0.519 | 0.136 | 0.148 | 0.029 |
| A3 | 0.038 | 0.050 | 0.147 | 0.123 | 0.010 | 0.018 | 0.165 | 0.148 |
| A4 | 0.048 | 0.053 | 0.174 | 0.141 | 0.006 | 0.023 | 0.144 | 0.123 |
| A5 | 0.053 | 0.057 | 0.072 | 0.063 | 0.084 | 0.085 | 0.069 | 0.041 |
| A6 | 0.795 | 0.655 | 0.614 | 0.381 | 0.824 | 0.837 | 0.630 | 0.275 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.179 | 0.034 | 0.140 | 0.090 | 0.071 | 0.078 | 0.064 | 0.075 |
| A1 | 0.028 | 0.086 | 0.078 | 0.107 | 0.040 | 0.053 | 0.077 | 0.064 |
| A2 | 0.120 | 0.001 | 0.130 | 0.046 | 0.180 | 0.116 | 0.115 | 0.009 |
| A3 | 0.028 | 0.030 | 0.067 | 0.093 | 0.010 | 0.008 | 0.076 | 0.065 |
| A4 | 0.032 | 0.102 | 0.076 | 0.102 | 0.006 | 0.003 | 0.088 | 0.095 |
| A5 | 0.018 | 0.031 | 0.082 | 0.101 | 0.024 | 0.028 | 0.073 | 0.079 |
| A6 | 0.265 | 0.000 | 0.275 | 0.067 | 0.418 | 0.812 | 0.294 | 0.004 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.239 | 0.258 | 0.140 | 0.133 | 0.068 | 0.071 | 0.059 | 0.096 |
| A1 | 0.048 | 0.073 | 0.136 | 0.093 | 0.059 | 0.058 | 0.097 | 0.098 |
| A2 | 0.312 | 0.254 | 0.216 | 0.003 | 0.421 | 0.068 | 0.140 | 0.003 |
| A3 | 0.036 | 0.045 | 0.112 | 0.083 | 0.011 | 0.015 | 0.115 | 0.098 |
| A4 | 0.030 | 0.057 | 0.127 | 0.095 | 0.017 | 0.008 | 0.117 | 0.119 |
| A5 | 0.019 | 0.037 | 0.051 | 0.047 | 0.059 | 0.065 | 0.051 | 0.036 |
| A6 | 0.640 | 0.139 | 0.544 | 0.007 | 0.897 | 0.864 | 0.562 | 0.008 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.101 | 0.098 | 0.081 | 0.093 | 0.041 | 0.032 | 0.057 | 0.085 |
| A1 | 0.072 | 0.090 | 0.230 | 0.173 | 0.075 | 0.083 | 0.203 | 0.210 |
| A2 | 0.686 | 0.698 | 0.237 | 0.178 | 0.641 | 0.345 | 0.203 | 0.063 |
| A3 | 0.028 | 0.043 | 0.157 | 0.124 | 0.011 | 0.008 | 0.152 | 0.140 |
| A4 | 0.059 | 0.082 | 0.204 | 0.172 | 0.022 | 0.020 | 0.184 | 0.162 |
| A5 | 0.078 | 0.098 | 0.113 | 0.108 | 0.059 | 0.050 | 0.082 | 0.058 |
| A6 | 0.488 | 0.657 | 0.235 | 0.265 | 0.588 | 0.650 | 0.249 | 0.238 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.132 | 0.129 | 0.085 | 0.093 | 0.038 | 0.032 | 0.052 | 0.083 |
| A1 | 0.087 | 0.073 | 0.401 | 0.300 | 0.106 | 0.119 | 0.351 | 0.382 |
| A2 | 0.906 | 0.803 | 0.275 | 0.213 | 0.775 | 0.481 | 0.230 | 0.058 |
| A3 | 0.027 | 0.024 | 0.264 | 0.180 | 0.007 | 0.007 | 0.280 | 0.225 |
| A4 | 0.072 | 0.053 | 0.328 | 0.235 | 0.025 | 0.031 | 0.268 | 0.235 |
| A5 | 0.115 | 0.105 | 0.143 | 0.123 | 0.062 | 0.058 | 0.104 | 0.074 |
| A6 | 0.733 | 0.758 | 0.287 | 0.311 | 0.793 | 0.865 | 0.325 | 0.315 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.112 | 0.082 | 0.098 | 0.109 | 0.067 | 0.065 | 0.071 | 0.091 |
| A1 | 0.042 | 0.041 | 0.145 | 0.113 | 0.052 | 0.045 | 0.104 | 0.125 |
| A2 | 0.490 | 0.356 | 0.216 | 0.067 | 0.493 | 0.207 | 0.175 | 0.010 |
| A3 | 0.027 | 0.022 | 0.120 | 0.097 | 0.012 | 0.006 | 0.099 | 0.091 |
| A4 | 0.031 | 0.020 | 0.128 | 0.114 | 0.007 | 0.003 | 0.109 | 0.101 |
| A5 | 0.038 | 0.052 | 0.072 | 0.070 | 0.043 | 0.047 | 0.052 | 0.043 |
| A6 | 0.837 | 0.492 | 0.623 | 0.083 | 0.900 | 0.901 | 0.628 | 0.024 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.151 | 0.143 | 0.100 | 0.098 | 0.054 | 0.055 | 0.063 | 0.094 |
| A1 | 0.058 | 0.057 | 0.253 | 0.165 | 0.064 | 0.070 | 0.201 | 0.191 |
| A2 | 0.721 | 0.694 | 0.257 | 0.167 | 0.693 | 0.313 | 0.182 | 0.035 |
| A3 | 0.024 | 0.033 | 0.173 | 0.127 | 0.013 | 0.012 | 0.140 | 0.114 |
| A4 | 0.036 | 0.039 | 0.195 | 0.146 | 0.018 | 0.021 | 0.185 | 0.141 |
| A5 | 0.081 | 0.080 | 0.102 | 0.088 | 0.061 | 0.063 | 0.065 | 0.038 |
| A6 | 0.956 | 0.970 | 0.789 | 0.467 | 0.959 | 0.964 | 0.804 | 0.476 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.146 | 0.022 | 0.130 | 0.079 | 0.085 | 0.089 | 0.087 | 0.078 |
| A1 | 0.036 | 0.072 | 0.085 | 0.097 | 0.032 | 0.033 | 0.070 | 0.080 |
| A2 | 0.275 | 0.104 | 0.243 | 0.026 | 0.267 | 0.079 | 0.175 | 0.010 |
| A3 | 0.027 | 0.032 | 0.082 | 0.090 | 0.018 | 0.004 | 0.078 | 0.088 |
| A4 | 0.022 | 0.042 | 0.081 | 0.089 | 0.006 | 0.004 | 0.073 | 0.080 |
| A5 | 0.009 | 0.017 | 0.032 | 0.027 | 0.011 | 0.010 | 0.036 | 0.035 |
| A6 | 0.355 | 0.097 | 0.321 | 0.063 | 0.428 | 0.365 | 0.335 | 0.004 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.151 | 0.183 | 0.119 | 0.127 | 0.081 | 0.080 | 0.077 | 0.109 |
| A1 | 0.036 | 0.063 | 0.101 | 0.084 | 0.038 | 0.032 | 0.073 | 0.83 |
| A2 | 0.399 | 0.322 | 0.186 | 0.002 | 0.482 | 0.145 | 0.183 | 0.003 |
| A3 | 0.027 | 0.066 | 0.120 | 0.082 | 0.018 | 0.005 | 0.107 | 0.100 |
| A4 | 0.021 | 0.055 | 0.116 | 0.097 | 0.010 | 0.005 | 0.089 | 0.092 |
| A5 | 0.022 | 0.023 | 0.050 | 0.029 | 0.032 | 0.041 | 0.034 | 0.030 |
| A6 | 0.673 | 0.097 | 0.610 | 0.004 | 0.977 | 0.960 | 0.617 | 0.004 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.069 | 0.072 | 0.051 | 0.062 | 0.059 | 0.067 | 0.044 | 0.062 |
| A1 | 0.061 | 0.046 | 0.309 | 0.211 | 0.058 | 0.048 | 0.328 | 0.240 |
| A2 | 0.813 | 0.744 | 0.297 | 0.242 | 0.769 | 0.549 | 0.279 | 0.166 |
| A3 | 0.031 | 0.029 | 0.218 | 0.150 | 0.016 | 0.009 | 0.221 | 0.136 |
| A4 | 0.071 | 0.054 | 0.281 | 0.221 | 0.041 | 0.032 | 0.286 | 0.215 |
| A5 | 0.148 | 0.133 | 0.248 | 0.214 | 0.093 | 0.071 | 0.168 | 0.124 |
| A6 | 0.650 | 0.735 | 0.255 | 0.305 | 0.656 | 0.735 | 0.295 | 0.388 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.061 | 0.083 | 0.053 | 0.054 | 0.038 | 0.046 | 0.048 | 0.054 |
| A1 | 0.101 | 0.047 | 0.494 | 0.367 | 0.102 | 0.065 | 0.572 | 0.442 |
| A2 | 0.979 | 0.933 | 0.345 | 0.265 | 0.949 | 0.837 | 0.336 | 0.188 |
| A3 | 0.034 | 0.023 | 0.331 | 0.234 | 0.018 | 0.011 | 0.364 | 0.259 |
| A4 | 0.106 | 0.068 | 0.408 | 0.297 | 0.045 | 0.044 | 0.439 | 0.336 |
| A5 | 0.207 | 0.165 | 0.251 | 0.237 | 0.083 | 0.064 | 0.196 | 0.180 |
| A6 | 0.929 | 0.933 | 0.320 | 0.379 | 0.936 | 0.933 | 0.359 | 0.407 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.083 | 0.047 | 0.081 | 0.095 | 0.078 | 0.047 | 0.068 | 0.093 |
| A1 | 0.036 | 0.047 | 0.187 | 0.131 | 0.036 | 0.035 | 0.182 | 0.136 |
| A2 | 0.618 | 0.505 | 0.251 | 0.063 | 0.598 | 0.346 | 0.252 | 0.021 |
| A3 | 0.029 | 0.041 | 0.136 | 0.110 | 0.023 | 0.015 | 0.141 | 0.100 |
| A4 | 0.043 | 0.053 | 0.180 | 0.136 | 0.028 | 0.023 | 0.173 | 0.121 |
| A5 | 0.105 | 0.100 | 0.168 | 0.148 | 0.072 | 0.056 | 0.119 | 0.087 |
| A6 | 0.946 | 0.515 | 0.670 | 0.082 | 0.953 | 0.946 | 0.697 | 0.042 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.069 | 0.071 | 0.072 | 0.063 | 0.049 | 0.041 | 0.061 | 0.069 |
| A1 | 0.056 | 0.048 | 0.301 | 0.208 | 0.050 | 0.053 | 0.276 | 0.212 |
| A2 | 0.931 | 0.862 | 0.325 | 0.286 | 0.901 | 0.691 | 0.291 | 0.176 |
| A3 | 0.031 | 0.039 | 0.221 | 0.149 | 0.018 | 0.014 | 0.214 | 0.147 |
| A4 | 0.065 | 0.057 | 0.236 | 0.193 | 0.030 | 0.029 | 0.238 | 0.200 |
| A5 | 0.195 | 0.162 | 0.191 | 0.189 | 0.120 | 0.089 | 0.158 | 0.146 |
| A6 | 1.000 | 0.999 | 0.850 | 0.604 | 1.000 | 0.999 | 0.875 | 0.584 |
| UES | UVaR | CES(5) | CVaR(5) | MUES | MUVaR | MCES(5) | MCVaR(5) | |
| n=250, Size and Power(size-corrected) | ||||||||
| H0 | 0.103 | 0.093 | 0.101 | 0.082 | 0.098 | 0.089 | 0.095 | 0.071 |
| A1 | 0.029 | 0.077 | 0.078 | 0.097 | 0.027 | 0.027 | 0.067 | 0.057 |
| A2 | 0.400 | 0.527 | 0.344 | 0.050 | 0.290 | 0.027 | 0.202 | 0.000 |
| A3 | 0.023 | 0.088 | 0.088 | 0.088 | 0.018 | 0.000 | 0.079 | 0.084 |
| A4 | 0.034 | 0.082 | 0.100 | 0.082 | 0.017 | 0.005 | 0.102 | 0.100 |
| A5 | 0.055 | 0.055 | 0.100 | 0.055 | 0.013 | 0.003 | 0.052 | 0.024 |
| A6 | 0.401 | 0.956 | 0.349 | 0.062 | 0.420 | 0.955 | 0.353 | 0.001 |
| n=500, Size and Power(size-corrected) | ||||||||
| H0 | 0.075 | 0.124 | 0.090 | 0.095 | 0.062 | 0.103 | 0.082 | 0.092 |
| A1 | 0.030 | 0.040 | 0.123 | 0.083 | 0.028 | 0.029 | 0.107 | 0.090 |
| A2 | 0.732 | 0.606 | 0.360 | 0.051 | 0.720 | 0.292 | 0.249 | 0.001 |
| A3 | 0.033 | 0.058 | 0.133 | 0.092 | 0.022 | 0.005 | 0.124 | 0.114 |
| A4 | 0.036 | 0.054 | 0.156 | 0.120 | 0.021 | 0.009 | 0.141 | 0.124 |
| A5 | 0.117 | 0.058 | 0.133 | 0.101 | 0.071 | 0.040 | 0.100 | 0.082 |
| A6 | 1.000 | 0.967 | 0.648 | 0.002 | 1.000 | 0.995 | 0.657 | 0.002 |
由于小样本T存在size扭曲,我们汇报了size-corrected powers。其中,ES的无条件后验分析很好地识别了备择假设A2和A6,条件后验分析对备择假设A1和A6具有最大的检验效能(Power值最大),对备择假设A2-A5也具有一定的检验效果。在绝大多数情况下,CES(5)和MCES(5)有着比CVaR(5)和MCVaR(5)更大的检验效能(Power值更大)。最后,MUES和MCES(5)的检验效能随着样本外观测n的增加而变大,说明了这些检验对备择假设而言是满足一致性的。当模型的残差项服从其他分布时,比如说时变高阶距的Hansen-Skewed-t分布,也可以得到一致的结论。②
② 限于篇幅,没有汇报这些模拟结果,读者如有兴趣,可以向作者索取。
蒙特卡洛模拟的主要结论如下。当T很小时(T=250),基本后验分析存在显著的size扭曲,但这些扭曲会随着T的增加而显著下降(T=2 500)。与之相比,修正的后验分析对T的取值具有稳健性。由于检验统计量需要根据模型和估计量去修正,size的改善会导致计算成本的增加。所以,我们建议大家在样本内观测T很大时(T=2 500,n=250)采用基本后验分析方法,在样本内观测T较小时(T=250,n=250)采用修正的后验分析方法。
模拟检验结果也说明了,无条件后验分析和条件后验分析是互补的,而不是替代的。因此,我们建议在实践中同时使用两种后验分析方法。模拟结果也显示,相比于VaR的检验,基于ES的检验效能更好。在本文下一节,我们将采用2007年金融危机期间三大股指的真实数据,进一步验证我们的结论。
五、实证应用
我们通过采用2007年金融危机期间全球三大股票指数,来检验ES作为风险度量指标的优点。实证结果显示,VaR后验分析方法在金融危机时期不能拒绝常规风险模型(残差项服从Student-t分布的AR(1)-GARCH(1, 1)模型);但本文提出的ES后验分析方法能够在金融危机时期显著拒绝常规风险模型。我们的实证结果补充了Kourouma等(2011)及O’Brien和Szerszen(2014)的研究,他们分别以金融危机期间的股票指数和美国五大银行为研究对象,评估了传统后验分析的表现。为与之对比,我们将比较传统VaR后验分析和本文ES后验分析的表现。①
① 重复本文实证应用的R code,可以通过Run My Code网站获得(http://www.runmycode.org/)。
具体而言,本文采用S&P 500指数、DAX指数以及恒生指数的日度数据展开分析。数据通过finance.yahoo.com获得,时间期限是1997.1.1 -2009.6.30。表 10从样本内和样本外两个时间段对三大股指进行了描述统计,样本内时间是1991.1.1-2007.6.30,样本外时间是金融危机期间的2007.7.1-2009.6.30。概括地讲,股票指数呈现了尖峰后尾和波动率聚集的特点,并且这些特点在金融危机期间尤为明显。表 10显示,三大股指的超额峰度取值都很大,特别是1997年亚洲金融危机导致了恒生指数的超额峰度最大。图 1显示,三大股指的对数收益率存在波动率聚集现象,金融危机期间股指收益的波动更为明显,尤其是标普500指数在2008.7 -2009.3期间几乎下降了一半。在2001-2003年期间,由于911恐怖袭击和股市处于整体下行的阶段,S&P 500指数和DAX指数具有很大的波动。香港恒生指数则在1997年末经历了明显的波动。
| 样本内时间(1997-2007年) | 样本外时间(2007-2009年) | |||||
| S&P500 | DAX | Hangseng | S&P500 | DAX | Hangseng | |
| 观测值 | 2 639 | 2 658 | 2 596 | 504 | 509 | 503 |
| 均值 | 0.027 | 0.039 | 0.019 | -0.098 | -0.100 | -0.034 |
| 中位数 | 0.059 | 0.106 | 0.042 | 0.036 | 0.016 | 0.052 |
| 标准差 | 1.131 | 1.577 | 1.677 | 2.218 | 2.045 | 2.762 |
| 偏度 | -0.089 | -0.152 | 0.146 | -0.065 | 0.351 | 0.167 |
| 超额峰度 | 3.165 | 2.348 | 11.355 | 4.035 | 5.273 | 3.319 |
| 最大值 | 5.574 | 7.553 | 17.250 | 10.960 | 10.800 | 13.410 |
| 10分位点 | -1.324 | -2.132 | -1.712 | -2.478 | -2.132 | -3.238 |
| 5分位点 | -1.815 | -2.567 | -2.552 | -3.506 | -3.371 | -4.381 |
| 1分位点 | -2.881 | -4.547 | -4.306 | -6.310 | -6.061 | -7.305 |
| 最小值 | -7.113 | -6.652 | -14.73 | -9.470 | -7.433 | -13.580 |

|
| 图 1 三大股指的日均对数收益率 |
我们通过AR(1)-GARCH(1, 1)-t模型拟合对数收益Yt。在给定置信水平α,VaR和ES等于:VaRt(α)=-a0Yt-1-σtFv-1(α), σt2=ω0+α0σt-12εt-12+β0σt-12,ESt(α)=-a0Yt-1-σtm(α), m(α)=E[εt|εt≤Fv-1(α)]。
我们采用样本内数据通过CMLE方法估计未知参数,并采用样本外数据做后验分析。表 11汇报了位置参数的估计结果,包括Fv-1(α)和m(α)。①表 11显示,三大股指存在明显的波动率惯性现象。恒生指数的自由度参数最小,所以它的厚尾现象也最为明显,这与表 10中恒生指数有最大的峰度相一致。
① 本文中,我们将自由度参数处理成离散、未知的。那么,估计效应仅仅来源于位置参数和尺度参数的不确定性。Escanciano和Olmo(2010)有相似的发现。
| S&P500 | DAX | Hangseng | |
| a0 | -0.027 | 0.004 | 0.034 |
| ω0 | 0.007 | 0.016 | 0.010 |
| α0 | 0.059 | 0.088 | 0.058 |
| β0 | 0.937 | 0.910 | 0.948 |
| v | 9 | 10 | 4 |
| Fv-1(0.05) | -1.617 | -1.621 | -1.507 |
| Fv-1(0.01) | -2.488 | -2.472 | -2.649 |
| m(0.1) | -1.781 | -1.779 | -1.767 |
| m(0.25) | -2.544 | -2.521 | -2.824 |
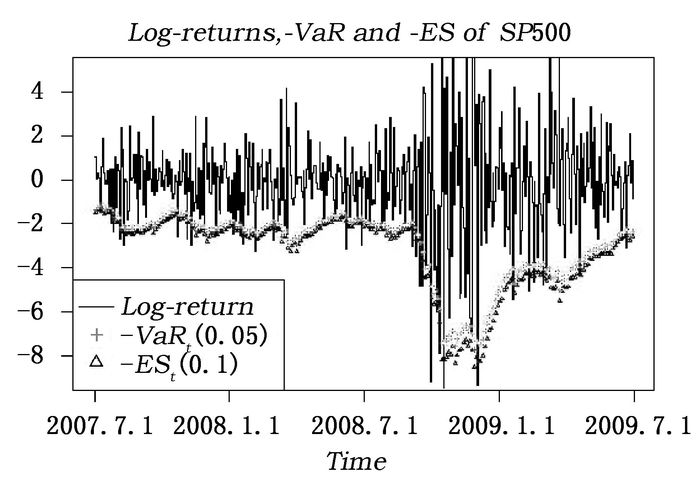
图 2-4分别绘制了S&P 500指数、DAX指数以及恒生指数的VaR(0.05)和ES(0.1)估计结果。从中可知,-ES(0.1)要小于-VaR(0.05)。当Yt低于-VaR(0.05)时,-ES(0.1)更加接近真实的Yt。以2008年9月15日为例,当天雷曼兄弟破产,S&P 500指数下降4.83%,模型估计出的VaR(0.05)是1.82%,ES(0.1)则是2.65%,所以ES估计值更加接近真实损失。S&P 500指数收益在2007.7.1 -2009.6.30期间共有504个观测值中,其中41个观测值小于-VaR(0.05)。在这41个观测值中,S&P 500指数的平均损失是3.82%,VaR(0.05)的平均值是2.79%,而ES(0.1)的平均值则是3.07%。另外,还有11个观测值小于-ES(0.1),S&P 500指数的平均损失是3.76%,VaR(0.05)的平均值是3.13%,而ES(0.1)的平均值则是3.20%。因此,ES比VaR更好地描述了极端损失,通过DAX和恒生指数也可以得到类似结论。
|
| 图 2 S&P 500指数的对数收益以及VaR和ES估计值 |
|
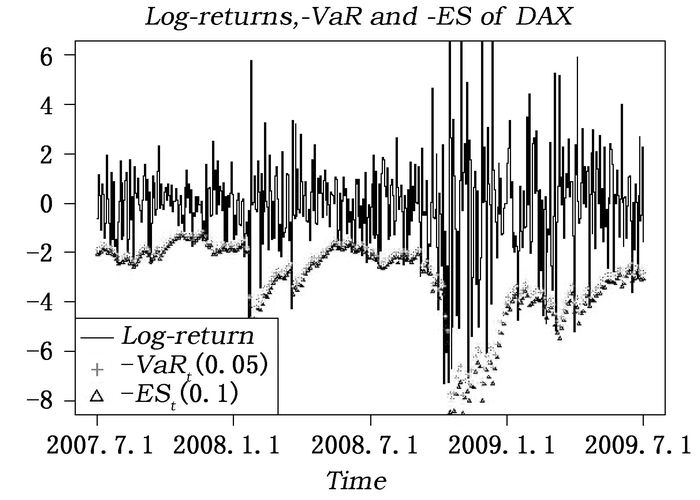
| 图 3 DAX指数的对数收益以及VaR和ES估计值 |
|
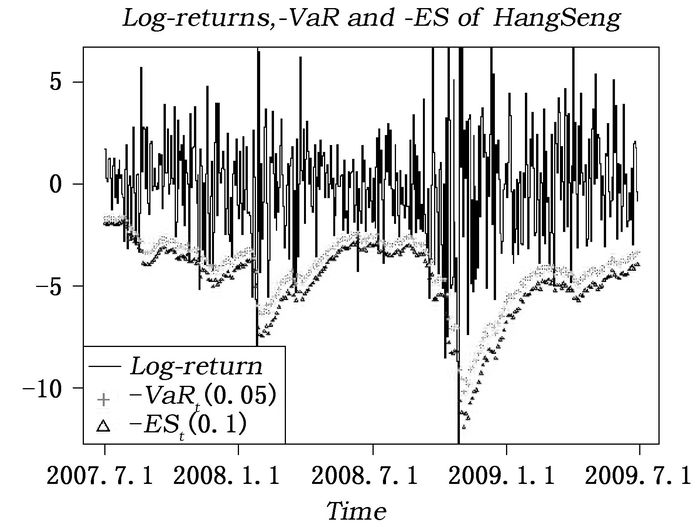
| 图 4 恒生指数的对数收益以及VaR和ES估计值 |
表 12汇报了2007年金融危机前后三大股票指数的碰撞序列取值
| 金融危机前(2005-2007年) | 金融危机后(2007-2009年) | |||||
| S&P500 | DAX | Hangseng | S&P500 | DAX | Hangseng | |
| V(0.05) | 20 | 20 | 24 | 41 | 35 | 29 |
| CV(0.1) | 20.309 | 22.434 | 24.714 | 40.026 | 34.862 | 30.612 |
| n×0.05 | 25.2 | 25.45 | 25.15 | 25.2 | 25.45 | 25.15 |
| V(0.01) | 5 | 8 | 2 | 11 | 5 | 5 |
| CV(0.025) | 6.110 | 6.360 | 4.063 | 13.702 | 9.101 | 6.145 |
| n×0.01 | 5.04 | 5.09 | 5.03 | 5.04 | 5.09 | 5.03 |
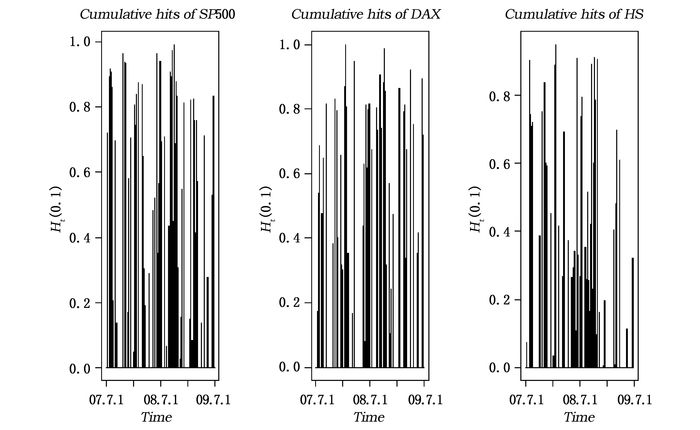
图 5描述了金融危机期间三大股票指数的累积碰撞序列{
|
| 图 5 金融危机期间三大股指的累积违背 |
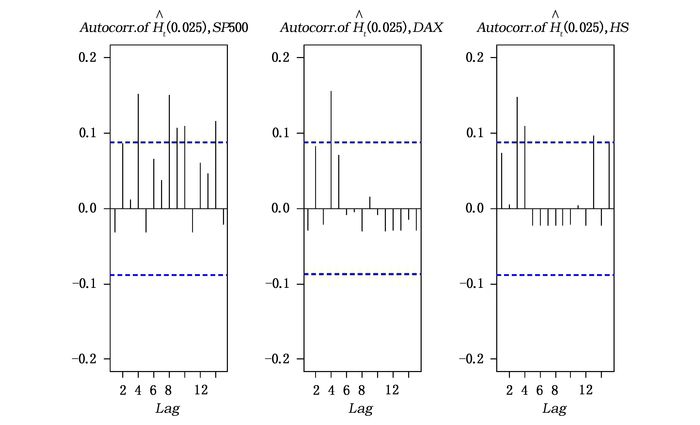
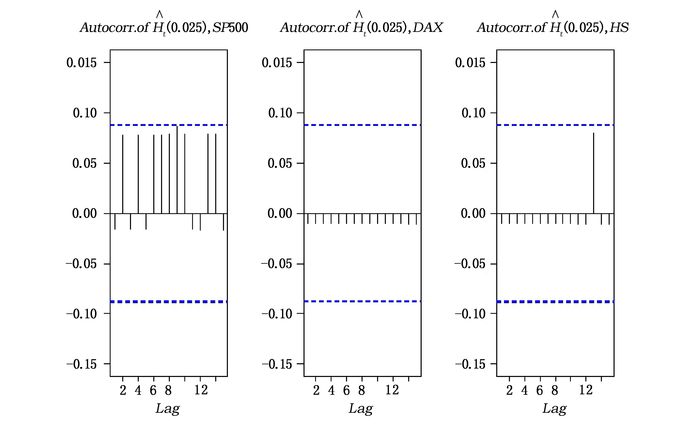
表 13汇报了三大股票指数无条件后验分析(UES、UVaR、MUES、MUVaR)以及条件后验分析(CES(5)、CVaR(5)、MCES(5)、MCVaR(5))的p值。ES的条件后验分析CES(5)和MCES(5)都拒绝了原假设中的风险模型,而VaR的条件后验分析CVaR(5)和MCVaR(5)则不能拒绝。图 6和图 7分别绘制了
| ES(0.025) | VaR(0.01) | ES(0.1) | VaR(0.05) | |
| S&P500 | ||||
| U | 0.011 | 0.070 | 0.004 | 0.010 |
| C(5) | 0.007 | 0.270 | 0.009 | 0.052 |
| MU | 0.019 | 0.073 | 0.006 | 0.013 |
| MC(5) | 0.017 | 0.271 | 0.010 | 0.053 |
| DAX | ||||
| U | 0.224 | 0.968 | 0.045 | 0.095 |
| C(5) | 0.002 | 0.998 | 0.091 | 0.768 |
| MU | 0.253 | 0.968 | 0.052 | 0.102 |
| MC(5) | 0.015 | 0.998 | 0.095 | 0.769 |
| Hangseng | ||||
| U | 0.939 | 0.989 | 0.194 | 0.462 |
| C(5) | 0.002 | 0.998 | 0.002 | 0.002 |
| MU | 0.945 | 0.990 | 0.310 | 0.509 |
| MC(5) | 0.003 | 0.998 | 0.004 | 0.002 |
| 注:U是基本的无条件后验分析,MU是稳健的无条件后验分析,C(5)是m=5的基本条件后验分析,MC(5)是m=5的稳健条件后验分析。 | ||||
|
|
图 6
三大股指的 |
|
|
图 7
三大股指的 |
图 7显示,三个股指序列的碰撞序列
另一方面,三个股指序列的累积碰撞序列
总之,基于VaR的后验分析,我们会认为正常时期建立的风险模型在金融危机发生后也是适用的,并且据此计算的存款准备金也是足够的。但是,如果采用ES度量风险,本文提出的后验分析方法可以明确地拒绝正常时期的风险模型。我们的实证分析证实了ES相比于VaR更具备理论优势(Artzer等,1997,1999),并且该理论优势也可以在市场风险的后验分析中获得经验证据。本文基于累积碰撞序列提出的一套后验分析方法,不仅有助于评估金融损失发生的可能性,也有助于发现金融损失的规模大小。
六、结论
尽管大量的理论证据表明,ES作为风险度量指标比VaR更具有优越性,但是直到最近金融机构和监管者才开始采用ES替换VaR。在这个转变过程中,一大挑战是没有工具可以用来评估ES模型(即,后验分析)。本文通过累积碰撞序列构建ES的无条件和条件后验分析,这也是基于碰撞序列对VaR进行后验分析的自然推广。但与碰撞序列不同,累积碰撞序列包括了尾部风险的信息,为风险提供了更加完整的描述。
本文提出了基本的无条件和条件后验分析方法和对估计风险保持稳健性的经修正的后验分析方法。无条件后验分析采用t检验对累积碰撞序列的均值进行假设检验,条件后验分析采用基于累积碰撞序列的Box-Pierce检验。同时,我们也建议大家采用累积碰撞序列的图形和自相关系数作为补充工具。在具体应用中,实践者需要对条件后验分析做出两个选择,分别是置信水平α和自相关阶数m。对于ES,我们建议选择α等于0.1、0.05或0.025,不建议取更小的值,因为此时需要很大的样本外观测才能对有限样本得到满意的渐进分布性质。关于自相关阶数的选择,我们选取了m=5。当然,一个合理的做法是通过数据驱动方法选择m(Escanciano和Labato,2009b)。该种方法在其他环境下被证明可以获得可靠的推论,它也可以用于本文情形中,从而以较小的计算成本获得数据驱动的ES后验分析。
附录A:假设
本节介绍检验方法所需的假设和一些公式。我们首先介绍一些符号。||·||表示欧几里德范数,C表示各个表达式中的一般常数,可以随表达式而变化。
为了完整性,我们将展示考虑了转换函数φ(ut)的一般化结果。φ∈
| $ \varphi \left( {{u_t}} \right) = \frac{1}{\alpha }\left( {\alpha - {u_t}} \right)1\left( {{u_t} \le {u_t}} \right) $ | (A.1) |
正文是在满足下述假设下对累计碰撞序列进行了分析,但在此附录中我们以一般化的φ∈
假设 A0:给定信息集Ωt-1,Yt的条件分布是G(·, Ωt-1, θ)。
假设 A1:{ Yt, Xt }t=-T+1n满足严平稳和遍历性。
假设 A2:
假设 A3:信息截尾(information truncation)的影响要满足,
| $ \mathop {\sup }\limits_{0 \in {\Theta _0}} \frac{1}{{\sqrt n }}\sum\limits_{t = 1}^n {\left| {\varphi \left( {G\left( {{Y_t},{{\mathit{\hat \Omega }}_{t - 1}},\theta } \right)} \right) - \varphi \left( {G\left( {Y,{\mathit{\Omega }_{t - 1}},\theta } \right)} \right)} \right|} = \left. {{O_P}\left( 1 \right)} \right|。$ |
假设 A4:Ft(θ, x)关于θ和x∈[0, 1]连续可微,并且关于vφ也几乎肯定连续可微,
| $ E\left[ {\mathop {\sup }\limits_{0 \in {\Theta _0},0 \le x \le 1} \left\| {\frac{{\partial {F_t}\left( {\theta ,x} \right)}}{{\partial x}}} \right\|} \right] < C\;{\rm{and}}\;E\left[ {\int_0^1 {\mathop {\sup }\limits_{0 \in {\Theta _0}} \left\| {\frac{{\partial {F_t}\left( {\theta ,x} \right)}}{{\partial x}}} \right\|d\varphi \left( x \right)} } \right] < C。$ |
其中,A0在文献中常用,它假设模型是正确设定的。该假设也可以放松到如下形式,但不会改变本文的理论。P(Yt≤y|Ωt-1)=G(y, Ωt-1, θ0) for all y≤G-1(α, Ωt-1, θ0)。
假设A1是为了阐述的方便。我们的结果,可以扩展到一些非平稳和非遍历性的序列中(Escanciano,2007)。大多数常用的估计量可以满足假设A2,比如(拟)极大似然估计量和广义距估计量(Bose,1998;Wu,2007)。假设A3是信息截取的影响,由于很久之前的观测数据不可获得,所以产生了信息截取问题。很多有限二阶距的时间序列模型都可以满足假设A3,包括平稳不可逆的ARMA过程、GARCH过程等等(Bai,2003;Hong和Li,2003)。马尔科夫过程则不需要该假设。假设A4是为了满足某些实证过程和大数定律的渐进同等连续性。
附录B:估计效应(Estimation Effect)的表达式
本节给出一般规模尺度模型中的
| $ {Y_t} = {\mu _t} + {\sigma _t}{\varepsilon _t} $ | (B.1) |
其中,μt=μ(Ωt-1, θ0)=E[Yt|Ωt-1],σt2=σ2(Ωt-1, θ0)=Var[Yt|Ωt-1];并且εt的累积分布函数是Gε(·),概率密度函数是gε(·)。
推导可得:
| $ \frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }} = {g_t}\left( {G_\varepsilon ^{ - 1}\left( x \right)} \right)\frac{{{{\dot u}_t} + G_\varepsilon ^{ - 1}\left( x \right){{\dot \sigma }_t}}}{{{\sigma _t}}} $ | (B.2) |
其中,
| $ \begin{array}{l} {R_{ES}} = \frac{1}{\alpha }E\left\{ {\int_0^\alpha {\frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }}dx} } \right\} = \frac{1}{\alpha }E\left\{ {\int_0^\alpha {{g_\varepsilon }\left( {G_\varepsilon ^{ - 1}\left( x \right)} \right)\frac{{{{\dot u}_t} + G_\varepsilon ^{ - 1}\left( x \right){{\dot \sigma }_t}}}{{{\sigma _t}}}dx} } \right\}\\ \;\;\;\;\;\; = \frac{1}{\alpha }E\left\{ {\int_{G_\varepsilon ^{ - 1}\left( 0 \right)}^{G_\varepsilon ^{ - 1}\left( \alpha \right)} {{g_\varepsilon }\left( z \right)\frac{{{{\dot u}_t} + z{{\dot \sigma }_t}}}{{{\sigma _t}}}d{G_\varepsilon }\left( z \right)} } \right\} = \frac{1}{\alpha }E\left\{ {{g_\varepsilon }\left( {{\varepsilon _t}} \right)1\left( {{\varepsilon _t} \le G_\varepsilon ^{ - 1}\left( \varepsilon \right)} \right)\frac{{{{\dot u}_t} + {\varepsilon _t}{{\dot \sigma }_t}}}{{{\sigma _t}}}} \right\}, \end{array} $ |
以及
其中,
| $ \begin{array}{l} {R_j} = \frac{1}{{{v_{ES}}\left( \alpha \right)}}E\left\{ {\left( {{H_{t - j}}\left( \alpha \right) - \alpha /2} \right)\int_0^\alpha {{g_\varepsilon }\left( {G_\varepsilon ^{ - 1}\left( x \right)} \right)\frac{{{{\dot u}_t} + G_\varepsilon ^{ - 1}\left( x \right){{\dot \sigma }_t}}}{{{\sigma _t}}}dx} } \right\}\\ \;\;\;\;\; = \frac{1}{{{v_{ES}}\left( \alpha \right)}}E\left\{ {\left( {{H_{t - j}}\left( \alpha \right) - \alpha /2} \right)\int_{G_\varepsilon ^{ - 1}\left( 0 \right)}^{G_\varepsilon ^{ - 1}\left( \alpha \right)} {{g_\varepsilon }\left( z \right)\frac{{{{\dot u}_t} + z{{\dot \sigma }_t}}}{{{\sigma _t}}}d{G_\varepsilon }\left( z \right)} } \right\}\\ \;\;\;\;\; = \frac{1}{{{v_{ES}}\left( \alpha \right)}}E\left\{ {\left( {{H_{t - j}}\left( \alpha \right) - \alpha /2} \right){g_\varepsilon }\left( {{\varepsilon _t}} \right)1\left( {{\varepsilon _t} \le G_\varepsilon ^{ - 1}\left( \varepsilon \right)} \right)\frac{{{{\dot u}_t} + {\varepsilon _t}{{\dot \sigma }_t}}}{{{\sigma _t}}}} \right\}, \end{array} $ |
其对应的可行估计是,
| $ {{\hat R}_j} = \frac{1}{{{v_{ES}}\left( \alpha \right)}}\frac{1}{{n - j}}\sum\limits_{t = j + 1}^n {\left( {{{\hat H}_{t - j}}\left( \alpha \right) - \alpha /2} \right){g_\varepsilon }\left( {{{\hat \varepsilon }_t}} \right)1\left( {{{\hat \varepsilon }_t} \le G_\varepsilon ^{ - 1}\left( \varepsilon \right)} \right)\frac{{{{\dot {\hat u}}_t} + {\varepsilon _t}{{\dot {\hat \sigma} }_t}}}{{{{\hat \sigma }_t}}}} 。$ |
类似地,对修正的VaR后验分析而言,我们有:
| $ {{\tilde R}_{VaR}} = \frac{{{g_\varepsilon }\left( {G_\varepsilon ^{ - 1}\left( \alpha \right)} \right)}}{n}\sum\limits_{t = 1}^n {\frac{{{{\dot {\hat u}}_t} + G_\varepsilon ^{ - 1}\left( \alpha \right){{\dot {\hat \sigma} }_t}}}{{{{\hat \sigma }_t}}}} , $ |
以及,
附录C:证明
对于一般化的定理1和定理2,我们将再给予证明。这种一般性体现在φ(ut),φ∈
定理 A1:在假设A0-A4下,
其中,σφ2=vφ+λR′φE[ltl′t]Rφ,Rφ=-E
证明定理A1:首先考虑没有信息截尾的情况。
如果G仅仅依赖于有限阶滞后的Yt和Xt,则不存在信息截尾的情形。可以从Escanciano和Olmo(2010)定理1的证明中得到类似的论据。在假设A0-A2以及A4下,
| $ \frac{1}{{\sqrt n }}\sum\limits_{t = 1}^n {\left[ {\varphi \left( {{{\hat u}_t}} \right) - E\left[ {\varphi \left( {{{\hat u}_t}} \right)} \right]\left| {{\Omega _{t - 1}}} \right.} \right]} - \frac{1}{{\sqrt n }}\sum\limits_{t = 1}^n {\left[ {\varphi \left( {{u_t}} \right) - E\left[ {\varphi \left( {{u_t}} \right)} \right]\left| {{\Omega _{t - 1}}} \right.} \right]} = {o_P}\left( 1 \right)。$ |
因此,
| $ \begin{array}{l} \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{{\hat u}_t}} \right) - {c_\varphi }} \right]} = \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{{\hat u}_t}} \right) - {c_\varphi }} \right]} + \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {{{\left( {{{\theta '}_T} - {\theta _0}} \right)}^\prime }\frac{{\partial E\left[ {\varphi \left( {{u_t}\left( {{{\tilde \theta }_T}} \right)} \right)\left| {{\Omega _{t - 1}}} \right.} \right]}}{{\partial \theta }} + {o_P}\left( 1 \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{u_t}} \right) - {c_\varphi }} \right]} + \sqrt \lambda \sqrt T {\left( {{{\hat \theta }_T} - {\theta _0}} \right)^\prime }\frac{1}{n}\sum\limits_{l = 1}^n {\frac{{\partial E\left[ {\varphi \left( {{u_t}\left( {{{\tilde \theta }_T}} \right)} \right)\left| {{\Omega _{t - 1}}} \right.} \right]}}{{\partial \theta }} + {o_P}\left( 1 \right)} , \end{array} $ |
其中,
| $ \frac{{\partial E\left[ {\varphi \left( {{u_t}\left( \theta \right)} \right)\left| {{\Omega _{t - 1}}} \right.} \right]}}{{\partial \theta }} = \frac{{\partial \left( {\int_0^1 {\varphi \left( x \right)d{F_t}\left( {\theta ,x} \right)} } \right)}}{{\partial \theta }} = - \frac{{\partial \int_0^1 {{F_t}\left( {\theta ,x} \right)d\varphi \left( x \right)} }}{{\partial \theta }}。$ |
因此,
| $ \begin{array}{l} \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{{\hat u}_t}} \right) - {c_\varphi }} \right]} = \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{u_t}} \right) - {c_\varphi }} \right]} \sqrt \lambda \sqrt T {\left( {{{\hat \theta }_T} - {\theta _0}} \right)^\prime }{R_\varphi } + {o_P}\left( 1 \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{\sqrt n }}\sum\limits_{t = 1}^n {\left[ {\varphi \left( {{u_t}} \right) - {c_\varphi }} \right]\sqrt \lambda {{R'}_\varphi }\frac{1}{{\sqrt T }}} \sum\limits_{t = - Y + 1}^0 {{l_t} + {o_P}\left( 1 \right)} \end{array} $ |
注意,等式右侧第一项依分布收敛于N(0, vφ),并且前两项的协方差为零,因为第一项是针对样本外观测的式子,第二项是针对样本内观测的式子。从而完成了定理A1的证明。
其次,考虑信息存在截尾的情形。
定义
| $ \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{{\hat u}_t}} \right) - {c_\varphi }} \right]} = \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{{\hat u}_t}} \right) - \varphi \left( {{{\tilde u}_t}} \right)} \right]} + \frac{1}{{\sqrt n }}\sum\limits_{l = 1}^n {\left[ {\varphi \left( {{{\tilde u}_t}} \right) - {c_\varphi }} \right]} 。$ |
假设A3隐含了上式的第一项是oP(1)。然后,针对没有信息截尾的
定理1、推论1以及推论3的证明,可以直接从定理A1中得出。
接下来,我们证明一般化的定理2,为此我们需要如下引理。定义,
| $ {R_{nj}}\left( {x,y} \right) = \frac{1}{{n - j}}\sum\limits_{t = 1 + j}^n {\left\{ {1\left( {{u_t} \le x} \right) - x} \right\}\left\{ {1\left( {{u_{t - j}} \le y} \right) - y} \right\}} $ |
| $ {{\hat R}_{nj}}\left( {x,y} \right) = \frac{1}{{n - j}}\sum\limits_{t = 1 + j}^n {\left\{ {1\left( {{{\hat u}_t} \le x} \right) - x} \right\}\left\{ {1\left( {{{\hat u}_{t - j}} \le y} \right) - y} \right\}} 。$ |
引理 A1:在假设A0-A4下,我们有:
| $ \mathop {\sup }\limits_{0 \le x \le 1,0 \le y \le 1} \left| {\sqrt {n - j} \left[ {{{\hat R}_{nj}}\left( {x,y} \right) - {R_{nj}}\left( {x,y} \right)} \right] - \sqrt \lambda \sqrt T {{\left( {{{\hat \theta }_T} - \theta } \right)}^\prime }{E_j}\left( {x,y} \right)} \right| = {o_P}\left( 1 \right), $ |
其中,Ej(x, y)=E
引理A1是Du(2015)定理1的一个特殊情形,所以省略此处的证明。
引理 A2:定义R(x, y)是[0, 1]2上的函数。对于任意的0≤y≤1都有R(, y)∈
| $ R \to \int_0^1 {\int_0^1 {\varphi \left( x \right)\varphi \left( y \right)R\left( {dx,dy} \right)} } $ |
证明引理A2:根据分部积分定理(Shiryaev,1996,pp206,定理11)以及R的定义,我们有
注意,下式对任意的R1,R2∈l([0, 1]2),以及∫|φ(dx)|<∞都成立。从而,完成了证明。
| $ \begin{array}{l} \left| {\int_0^1 {\int_0^1 {{R_1}\left( {x,y} \right)\varphi \left( {dx} \right)\varphi \left( {dy} \right)} } - \int_0^1 {\int_0^1 {{R_2}\left( {x,y} \right)\varphi \left( {dx} \right)\varphi \left( {dy} \right)} } } \right|\\ \le \sup \left| {{R_1}\left( {x,y} \right) - {R_2}\left( {x,y} \right)} \right|\int_0^1 {\int_0^1 {\left| {\varphi \left( {dx} \right)\varphi \left( {dy} \right)} \right|} } , \end{array} $ |
在表述了两个引理之后,我们将证明一般化的定理2。定义φ(ut)滞后j阶(j>0)的自协方差和自相关系数是γj=Cov(φ(ut), φ(ut-j))和ρj=
| $ {{\hat \gamma }_{nj}} = \frac{1}{{n - j}}\sum\limits_{l = 1 + j}^n {\left( {\varphi \left( {{{\hat u}_t}} \right) - {c_t}} \right)\left. {\left( {\varphi \left( {{{\hat u}_{t - j}}} \right) - {c_t}} \right)} \right)} \;和\;{{\hat \rho }_{nj}} = \frac{{{{\hat \gamma }_{nj}}}}{{{{\hat \gamma }_{n0}}}}。$ |
定理 A2:在假设A0-A4下,
其中,Rj见下式,δij是克罗内克函数,δij在i=j时取值1,否则取值0。
| $ {R_j} = \frac{{ - 1}}{{{v_\varphi }}}E\left\{ {\left( {\varphi \left( {{u_{t - j}}} \right) - {c_\varphi }} \right)\int_0^1 {\frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }}d\varphi \left( x \right)} } \right\} $ | (C.1) |
证明定理A2:首先考虑没有信息截尾的情形。
如果G仅仅依赖于有限阶滞后的Yt和Xt,则不存在信息截尾的情形。注意,
| $ \sqrt {n - j} {{\hat \gamma }_{nj}} = \sqrt {n - j} \int_0^1 {\int_0^1 {\varphi \left( x \right)\varphi \left( y \right){{\hat R}_{nj}}\left( {dx,dy} \right)} } $ |
| $ \sqrt {n - j} {\gamma _{nj}} = \sqrt {n - j} \int_0^1 {\int_0^1 {\varphi \left( x \right)\varphi \left( y \right){R_{nj}}\left( {dx,dy} \right)} } 。$ |
通过引理1和引理2可得,
| $ \sqrt {n - j} {{\hat \gamma }_{nj}} = \sqrt {n - j} {\gamma _{nj}} + \sqrt \lambda \sqrt T {\left( {{{\hat \theta }_T} - {\theta _0}} \right)^\prime }\int_0^1 {\int_0^1 {\varphi \left( x \right)\varphi \left( y \right){E_j}\left( {dx,dy} \right)} } + {o_P}\left( 1 \right) $ | (C.2) |
其中,
| $ \begin{array}{l} \int_0^1 {\int_0^1 {\varphi \left( x \right)\varphi \left( y \right){E_j}\left( {dx,dy} \right)} } = \int_0^1 {\int_0^1 {E\left\{ {\varphi \left( x \right)\frac{{{\partial ^2}{F_t}\left( {{\theta _0},x} \right)}}{{\partial x\partial \theta }}dx\varphi \left( y \right)\left[ {1\left( {{u_{t - j}} \le dy} \right) - dy} \right]} \right\}} } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}\int_0^1 {E\left\{ {\varphi \left( x \right)\frac{{{\partial ^2}{F_t}\left( {{\theta _0},x} \right)}}{{\partial x\partial \theta }}dx\left( {\varphi \left( {{u_{t - j}}} \right) - {c_\varphi }} \right)} \right\}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}E\left\{ {\int_0^1 {\varphi \left( x \right)\frac{{{\partial ^2}{F_t}\left( {{\theta _0},x} \right)}}{{\partial x\partial \theta }}dx\left( {\varphi \left( {{u_{t - j}}} \right) - {c_\varphi }} \right)} } \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}E\left\{ {\left[ {\varphi \left( x \right)\frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }}\left| {_0^1} \right. - \int_0^1 {\frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }}dx} } \right]\left( {\varphi \left( {{u_{t - j}}} \right) - {c_\varphi }} \right)} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }} - E\left\{ {\int_0^1 {\frac{{\partial {F_t}\left( {{\theta _0},x} \right)}}{{\partial \theta }}d\varphi \left( x \right)\left( {\varphi \left( {{u_{t - j}}} \right) - {c_\varphi }} \right)} } \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}{v_\varphi }{R_j} \end{array} $ |
(C.1)式定义了Rj。由假设A4可对上式进行期望与积分互换,分部积分原理参见Shiryaev(1996,pp.206)。
因此,我们证明了
然后,我们可得出,
| $ \sqrt {n - j} \left( {{{\hat \rho }_{nj}} - {\rho _{nj}}} \right) = \frac{{\sqrt {n - j} \left( {{{\hat \gamma }_{nj}} - {\gamma _{nj}}} \right)}}{{{v_\varphi }}} + {o_p}\left( 1 \right) = {{R'}_j}\sqrt \lambda \sqrt T \left( {{\theta _T} - {\theta _0}} \right) + {o_p}\left( 1 \right)。$ |
| $ \begin{array}{l} 因此,\sqrt {n - j} {{\hat \rho }_{nj}} = \sqrt {n - j} {\rho _{nj}} + {{R'}_j}\sqrt \lambda \sqrt T \left( {{\theta _T} - {\theta _0}} \right) + {o_p}\left( 1 \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{\sqrt {n - j} {v_\varphi }}}\sum\limits_{l = 1 + j}^n {\left( {\varphi \left( {{u_t}} \right) - {c_\varphi }} \right)\left( {\varphi \left( {{u_{t - j}}} \right) - {c_\varphi }} \right) + {{R'}_j}\sqrt \lambda \frac{1}{{\sqrt T }}\sum\limits_{l = - T + 1}^0 {{l_t} + {o_p}\left( 1 \right)} } 。\end{array} $ |
注意,
接下来,我们考虑存在信息截尾的情形。
定义
| $ \sqrt {n - j} \left( {{{\hat \gamma }_{nj}} - {\gamma _{nj}}} \right) = \sqrt {n - j} \left( {{{\hat \gamma }_{nj}} - {{\tilde \gamma }_{nj}}} \right) + \sqrt {n - j} \left( {{{\tilde \gamma }_{nj}} - {\gamma _{nj}}} \right)。$ |
通过证明可知,上式中的第一项是op(1)。因为,
| $ \begin{array}{l} \sqrt {n - j} \left( {{{\hat \gamma }_{nj}} - {{\tilde \gamma }_{nj}}} \right) = \frac{1}{{\sqrt {n - j} }}\sum\limits_{l = 1 + j}^n {\left[ {\left( {\varphi \left( {{{\hat u}_t}} \right) - {c_\varphi }} \right)\left( {\varphi \left( {{{\hat u}_{t - j}}} \right) - {c_\varphi }} \right)\left( {\varphi \left( {{{\tilde u}_t}} \right) - {c_\varphi }} \right)\left( {\varphi \left( {{{\tilde u}_{t - j}}} \right) - {c_\varphi }} \right)} \right]} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{\sqrt {n - j} }}\sum\limits_{l = 1 + j}^n {\left( {\varphi \left( {{{\hat u}_t}} \right) - \varphi \left( {{{\tilde u}_t}} \right)} \right)\left( {\varphi \left( {{{\hat u}_{t - j}}} \right) - {c_\varphi }} \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{1}{{\sqrt {n - j} }}\sum\limits_{l = 1 + j}^n {\left( {\varphi \left( {{{\tilde u}_t}} \right) - {c_\varphi }} \right)\left( {\varphi \left( {{{\hat u}_{t - j}}} \right) - \varphi \left( {{{\tilde u}_{t - j}}} \right)} \right)} 。\end{array} $ |
以及从假设A3可知,φ(
定理2的证明:定义∑ =QΛQ′,其中Q是正交矩阵,Λ是对角矩阵,对角线元素是{π}j=1m。从定理A2可知,
推论2和推论4可从定理2得出。
| [1] | Acerbi C, Tasche D. On the coherence of expected shortfall[J]. Journal of Banking & Finance, 2002, 26(7): 1487–1503. |
| [2] | Acerbi C, Szekely B. Backtesting expected shortfall[N]. Risk Magazine, 2014. |
| [3] | Artzner P, Delbaen F, Eber M., et al. Thinking coherently[J]. Risk, 1997, 10: 68–71. |
| [4] | Artzner P, Delbaen F, Eber M., et al. Coherent measures of risk[J]. Mathematical Finance, 1999, 9(3): 203–226. DOI:10.1111/mafi.1999.9.issue-3 |
| [5] | Bai J. Testing parametric conditional distributions of dynamic models[J]. Review of Economics and Statistics, 2003, 85(3): 531–549. DOI:10.1162/003465303322369704 |
| [6] | Basak S, Shapiro A. Value-at-risk based risk management:Optimal policies and asset prices[J]. Review of Financial Studies, 2001, 14(2): 371–405. DOI:10.1093/rfs/14.2.371 |
| [7] | Basel Committee on Banking Supervision. Consultative document:Fundamental review of the trading book[R]. Basel, Switzerland, 2012. |
| [8] | Berkowitz J. Testing density forecasts with applications to risk management[J]. Journal of Business and Economic Statistics, 2001, 19(4): 465–474. DOI:10.1198/07350010152596718 |
| [9] | Berkowitz J, Christoffersen P, Pelletier D. Evaluating value-at-risk models with desk-level data[J]. Management Science, 2011, 57(12): 2213–2227. DOI:10.1287/mnsc.1080.0964 |
| [10] | Bose A. Bahadur representation of mestimates[J]. Annals of Statistics, 1998, 26(2): 771–777. DOI:10.1214/aos/1028144859 |
| [11] | Box G, Pierce D. Distribution of residual autocorrelations in autoregressive integrated moving average time series models[J]. Journal of American Statistical Association, 1970, 65(332): 1509–1527. DOI:10.1080/01621459.1970.10481180 |
| [12] | Christoffersen P. Evaluating interval forecasts[J]. International Economic Review, 1998, 39(4): 841–862. DOI:10.2307/2527341 |
| [13] | Christoffersen P, Goncalves P. Estimation risk in financial risk management[J]. Journal of Risk, 2005, 7(3): 1–28. DOI:10.21314/JOR.2005.112 |
| [14] | Christoffersen P. Value-at-risk models[M]. 2009. |
| [15] | Colletaz G, Hurlin C, Perignon C. The risk map:A new tool for validating risk models[J]. Journal of Banking and Finance, 2013, 37(10): 3843–3854. DOI:10.1016/j.jbankfin.2013.06.006 |
| [16] | Du Z. Nonparametric bootstrap tests for the independence of generalized errors[R]. CAEPR Working Paper No. 023-2009, 2015. |
| [17] | Emmer S, Kratz M, Tasche D. What is the best risk measure in practice? A comparison of standard measures[R]. ESSEC Business School:Paris, France, 2014. |
| [18] | Escanciano J. Weak convergence of non-stationary multivariate marked processes with applications to martingale testing[J]. Journal of Multivariate Analysis, 2007, 98(7): 1321–1336. DOI:10.1016/j.jmva.2007.03.004 |
| [19] | Escanciano J, Lobato I. Testing the martingale hypothesis[M]. 2009a. |
| [20] | Escanciano J, Lobato I. An automatic portmanteau test for serial correlation[J]. Journal of Econometrics, 2009b, 151(2): 140–149. DOI:10.1016/j.jeconom.2009.03.001 |
| [21] | Escanciano J, Olmo J. Backtesting parametric value-at-risk with estimation risk[J]. Journal of Business and Economic Statistics, 2010, 28(1): 36–51. DOI:10.1198/jbes.2009.07063 |
| [22] | Escanciano J, Velasco C. Specification tests of parametric dynamic conditional quantiles[J]. Journal of Econometrics, 2010, 159(1): 209–221. DOI:10.1016/j.jeconom.2010.06.003 |
| [23] | Escanciano J, Pei P. Pitfalls in backtesting historical simulation models[J]. Journal of Banking and Finance, 2012, 36(8): 2233–2244. DOI:10.1016/j.jbankfin.2012.04.004 |
| [24] | Francq C, Zakoian J. Risk-parameter estimation in volatility models[J]. Journal of Econometrics, 2015, 184(1): 158–173. DOI:10.1016/j.jeconom.2014.06.019 |
| [25] | Gourieroux C, Zakoian J. Estimation-adjusted VaR[J]. Econometric Theory, 2013, 29(4): 735–770. DOI:10.1017/S0266466612000680 |
| [26] | Hansen B. Autoregressive conditional density estimation[J]. International Economic Review, 1994, 35(3): 705–730. DOI:10.2307/2527081 |
| [27] | Hong Y, Lee T. Diagnostic checking for adequacy of linear and nonlinear time series models[J]. Econometric Theory, 2003, 19(6): 1065–1121. |
| [28] | Hong Y, Li H. Nonparametric specification testing for continuous-time modelswith applications to term structure of interest rates[J]. The Review of Financial Studies, 2005, 18(1): 37–84. DOI:10.1093/rfs/hhh006 |
| [29] | Hurlin C, Tokpavi S. Backtesting value-at-risk accuracy:A simple new test[J]. Journal of Risk, 2007, 9(9): 19–37. |
| [30] | Jorion P. Value at risk:The new benchmark for managing financial risk[M]. New York: McGraw-Hill, 2006. |
| [31] | Kerkhof J, Melenberg B. Backtesting for risk-based regulatory capital[J]. Journal of Banking and Finance, 2004, 28(8): 1845–1865. DOI:10.1016/j.jbankfin.2003.06.007 |
| [32] | Kourouma L, Dupre D, Sanfilippo G, et al. Extreme value at risk and expected shortfall during financial crisis[R]. Working Paper, 2011. |
| [33] | Kupiec P. Techniques for verifying the accuracy of risk measurement models[J]. The Journal of Derivatives, 1995, 3(2): 73–84. DOI:10.3905/jod.1995.407942 |
| [34] | McNeil A, Frey R. Estimation of tail-related risk measures for heteroscedastic financial time series:An extreme value approach[J]. Journal of Empirical Finance, 2000, 7(3/4): 271–300. |
| [35] | O'Brien J, Szerszen P. An evaluation of bank VaR measures for market risk during and before the financial crisis[R]. FEDS Working Paper No. 2014-21, 2014. |
| [36] | Perignon C, Smith D. A new approach to comparing VaR estimation methods[J]. Journal of Derivatives, 2008, 16(2): 54–66. DOI:10.3905/JOD.2008.16.2.054 |
| [37] | Rosenblatt M. Remarks on a multivariate transformation[J]. Annals of Mathematical Statistics, 1952, 23: 470–472. DOI:10.1214/aoms/1177729394 |
| [38] | Shiryaev A. Probability[M]. New York: Springer, 1996. |
| [39] | van der Vaart A, Wellner J. Weak convergence and empirical processes[M]. New York: Springer, 1996. |
| [40] | Wong W. Backtesting trading risk of commercial banks using expected shortfall[J]. Journal of Banking & Finance, 2008, 32(7): 1404–1415. |
| [41] | Wong W. Backtesting value-at-risk based on tail losses[J]. Journal of Empirical Finance, 2010, 17(3): 526–538. DOI:10.1016/j.jempfin.2009.11.004 |
| [42] | Wu W. M-estimation of linear models with dependent errors[J]. Annals of Statistics, 2007, 35(2): 495–521. DOI:10.1214/009053606000001406 |
| [43] | Yamai Y, Yoshiba T. Comparative analyses of expected shortfall and value-at-risk:Their estimation error, decomposition, and optimization[J]. Monetary and Economic Studies, 2002, 20(3): 87–122. |
| [44] | Yamai Y, Yoshiba T. Value-at-risk versus expected shortfall:A practical perspective[J]. Journal of Banking and Finance, 2005, 29(4): 99–115. |
 2017, Vol. 43
2017, Vol. 43


